Implementation
The Pink Cloud Antibes, 1916, Paul Signac
1. What is Implementation?
Implementation is the process of converting an algorithm in your head into source code.
Example of implementation type problem is:
- The algorithm is simple, but the code becomes excessively long.
- Problems dealing with real numbers and outputting to a certain number of decimal places.
- Problems that have to be dealt with by breaking strings according to certain criteria.
- The problem of finding and using the appropriate library.
There are many similarities between the type Simulation , Implementation, and Brute-Force in coding tests.
2. Implementation Example Problem
2.1 Problem : Left, Right, Up, Down
Traveler A stands on a square space of size N × N. This space is divided into squares of size 1 × 1.
The upper-left coordinate corresponds to (1, 1), and the lower-right coordinate corresponds to (N, N).
Traveler A can move up, down, left and right, and the starting coordinate is always (1, 1). In front of us is a plan with traveler A’s plans to move.
In the plan, one letter of L, R, U, and D is repeatedly written on one line based on space. The meaning of each character is as follows.
L: move one space to the left
R: move one space to the right
U: move up one space
D: move down one space
In this case, the movement of traveler A outside the square space of size N × N is ignored.
For example, if L or U is encountered at position (1, 1), it is ignored.
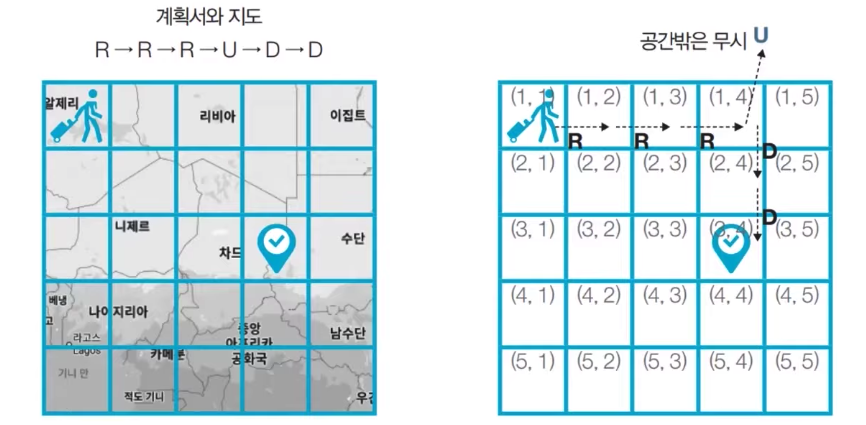the map and plan for N = 5
Difficulty: 1 | Solving Time: 15 minutes | Timeout: 2 seconds | Memory limit: 128 MB
Input conditions
The first line is given an N indicating the size of the space. (1<=N<=100)
In the second line, the contents of the travel plan for traveler A are given. (1<=Number of moves<=100)
Output conditions
In the first line, print the number written on the card selected according to the rules of the game.
| Input Example | Output Example |
5 | 3 4 |
R R R U D D |
2.2 Solution : Left, Right, Up, Down
This is a problem that needs to implement faithfully according to the requirements.
# title: 'LeftRightUpDown.py'
# Get N input
n = int(input())
x, y = 1, 1
plans = input(). split()
# Direction of movement according to L, R, U, D
dx = [0, 0, -1, 1]
dy = [-1, 1, 0, 0]
move_types = ['L', 'R', 'U', 'D']
# Check the move plans one by one
for plan in plans:
# Get coordinates after moving
for i in range(len(move_types)):
if plan == move_types[i]:
nx = x + dx[i]
ny = y + dy[i]
# Ignore if out of space
if nx < 1 or ny < 1 or nx > n or ny > n:
continue
# Perform a move
x, y = nx, ny
print(x, y)
2.3 Problem : Royal Knight
When the position of the knight on the 8 × 8 coordinate plane is given, the number of cases in which the knight can move is output. A knight can move from a specific location in the following two cases:
- Move two spaces horizontally and then move one space vertically
- Move two spaces vertically and then move one space horizontally
Write a program. In the royal garden, row positions are expressed as 1 to 8, and column positions are expressed as express from a to h.
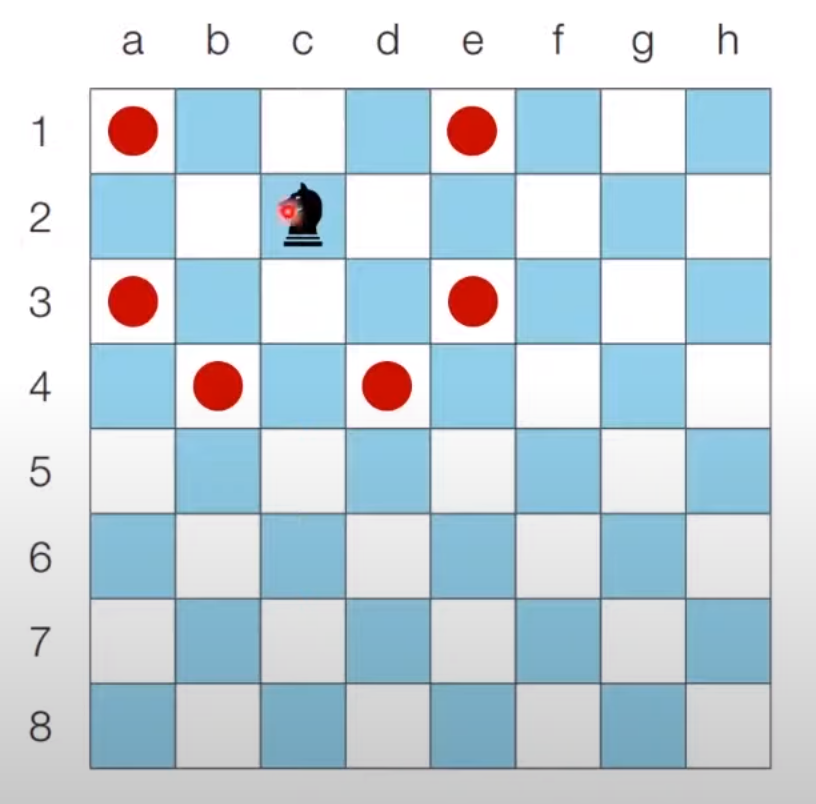
There are 6 possible moves when in c2.
There are 2 possible moves when in a1.
Difficulty: 1 | Solving Time: 20 minutes | Timeout: 1 second | Memory limit: 128 MB
Input conditions
In the first line, a two-character string representing the coordinates of where the knight is currently located on the 8x8 coordinate plane is entered. Input characters consist of columns and rows, like a1.
Output conditions
In the first line, print the number of times a knight can move.
| Input Example | Output Example |
| a1 | 2 |
2.4 Solution : Royal Knight
Check the 8 paths of the knight one by one and check if it is possible to move to each location.
Using the list, define direction vectors for 8 directions.
# title: 'RoyalKnight.py'
# Get the current knight's location
input_data = input()
row = int(input_data[1])
column = int(ord(input_data[0])) - int(ord('a')) + 1
# Define 8 directions a knight can move
steps = [(-2, -1), (-1, -2), (1, -2), (2, -1), (2, 1), (1, 2), (-1, 2 ), (-2, 1)]
# Check if it is possible to move to each position in 8 directions
result = 0
for step in steps:
# Check the location you want to move
next_row = row + step[0]
next_column = column + step[1]
# If it is possible to move to that location, the count is increased.
if next_row >= 1 and next_row <= 8 and next_column >= 1 and next_column <= 8:
result += 1
print(result)
https://www.freecodecamp.org/
https://www.programiz.com/
https://www.geeksforgeeks.org/
https://blog.naver.com/PostList.naver?blogId=ndb796
이것이 코딩테스트다,2020,나동빈,한빛미디어