Dynamic Programming

The Golden Horn. Morning, 1907, Paul Signac.png
- 1. What is Dynamic Programming?
- 2. Tabulation vs Memoization
- 3 Fibonacci Sequence using Dynamic Programming
- 4 Dynamic Programming VS Divide and Conquer
- 5 Dynamic Programming Example Problem
1. What is Dynamic Programming?
Dynamic programming is a method to dramatically improve execution time efficiency by properly using memory. It saves already calculated results (small problems) in a separate memory area to avoid recalculation.
Dynamic programming can be used when the problem satisfies the following two conditions.
1. Obtimal Substructure :
A big problem can be divided into small problems, and the big problem can be solved by collecting the answers to the divided small problems.
2. Overlapping Subproblem :
You have to solve the same small problem over and over again.
2. Tabulation vs Memoization
2.1 Tabulation in Bottom-Up
In general, Dynamic programming can be implemented in two ways: Top-down and Bottom-up.
Tabulation is a bottom-up method for solving DP problems.
As the name itself suggests starting from the bottom and accumulating answers to the top.
Let’s describe a state for our DP problem to be dp[x] with dp[0] as base state and dp[n] as our destination state. So, we need to find the value of destination state i.e dp[n].
If we start our transition from our base state i.e dp[0] and follow our state transition relation to reach our destination state dp[n], we call it the Bottom-Up approach as it is quite clear that we started our transition from the bottom base state and reached the topmost desired state.
// Tabulated version to find factorial x.
int dp[MAXN];
// base case
int dp[0] = 1;
for (int i = 1; i< =n; i++)
{
dp[i] = dp[i-1] * i;
}
The above code clearly follows the bottom-up approach as it starts its transition from the bottom-most base case dp[0] and reaches its destination state dp[n]. Here, we may notice that the DP table is being populated sequentially and we are directly accessing the calculated states from the table itself and hence, we call it the tabulation method.
2.2 Memoization in Top-down
Memoization is a technique of memoizing the result once calculated in the memory space.
- If you call the same problem again, you get the result you noted.
- Also called Caching in that it records a value.
If we need to find the value for some state say dp[n] and instead of starting from the base state that i.e dp[0] we ask our answer from the states that can reach the destination state dp[n] following the state transition relation, then it is the top-down fashion of DP.
Here, we start our journey from the top most destination state and compute its answer by taking in count the values of states that can reach the destination state, till we reach the bottom-most base state.
// Memoized version to find factorial x.
// To speed up we store the values
// of calculated states
// initialized to -1
int dp[MAXN]
// return fact x!
int solve(int x)
{
if (x==0)
return 1;
if (dp[x]!=-1)
return dp[x];
return (dp[x] = x * solve(x-1));
}
As we can see we are storing the most recent cache up to a limit so that if next time we got a call from the same state we simply return it from the memory. So, this is why we call it memoization as we are storing the most recent state values.
In this case, the memory layout is linear that’s why it may seem that the memory is being filled in a sequential manner like the tabulation method, but you may consider any other top-down DP having 2D memory layout like Min Cost Path, here the memory is not filled in a sequential manner.
3 Fibonacci Sequence using Dynamic Programming
The Fibonacci Sequence is a sequence of the following form, and can be effectively calculated with dynamic programming.
\(1,1,2,3,5,8,13,21,34,55,89,...\) A recurrence relation means a relational expression between adjacent identities.
The Fibonacci sequence can be expressed as an recurrence relation as follows: \[a_n = a_{n-1} + a_{n-2},\quad a_1 = 1, \quad a_2 = 1\]
Solving the Fibonacci sequence with a simple recursive function has exponential time complexity. (The time complexity is too high.)
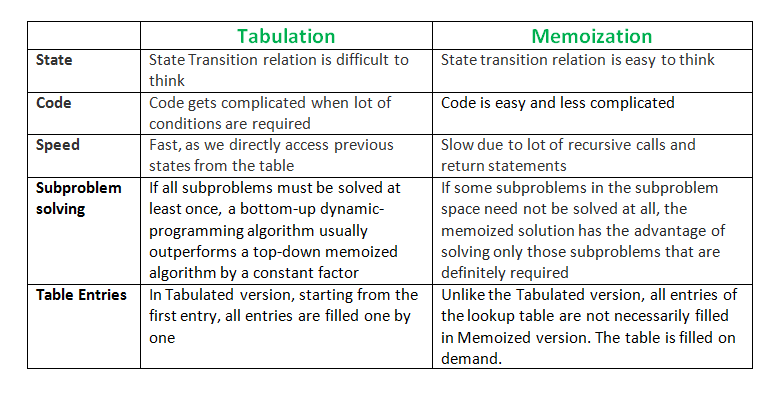
f(6)can be solved by finding f(5) and f(4) as above. -> 1. Optimal Substructure
Also, You can see that f(2) is called multiple times -> 2. Overlapping Subproblem
Therefore, the Fibonacci sequence can be implemented with dynamic programming!.
Fibonacci Sequence: Bottom-Up Dynamic Programming
# title : 'FibonacciBottomUp.py'
# Initialize the DP table to save the previously calculated result.
d = [0] * 100
# Reset the first and second Fibonacci numbers to 1.
d[1] = 1
d[2] = 1
n = 99
# Fibonacci Function implemented as a loop (bottom-up dynamic programming).
for i in range(3, n+1): #3 to nth
d[i] = d[i-1] + d[i-2] # Calculate all Fibonacci numbers, find each term in turn, start with the small problem.
print(d[n]) # 218922995834555169026
Fibonacci Sequence: Top-Down Dynamic Programming
# title : 'FibonacciTopDown.py'
# Initialize the list to memoize the calculated result.
d = [0] * 100
# Implementation of the Fibonacci function as a recursive function (top-down dynamic programming).
def fibo(x):
# Exit condition (return 1 if 1 or 2)
if x== 1 or x == 2:
return 1
# If the problem has already been calculated, return it as is.
if d[x] != 0:
return d[x]
# If it is a problem that has not been calculated yet, the Fibonacci result is returned according to the recurrence relation
d[x] = fibo(x-1) + fibo(x-2) # Write the added value to the list.
return d[x]
print(fibo(99)) # 218922995834555169026
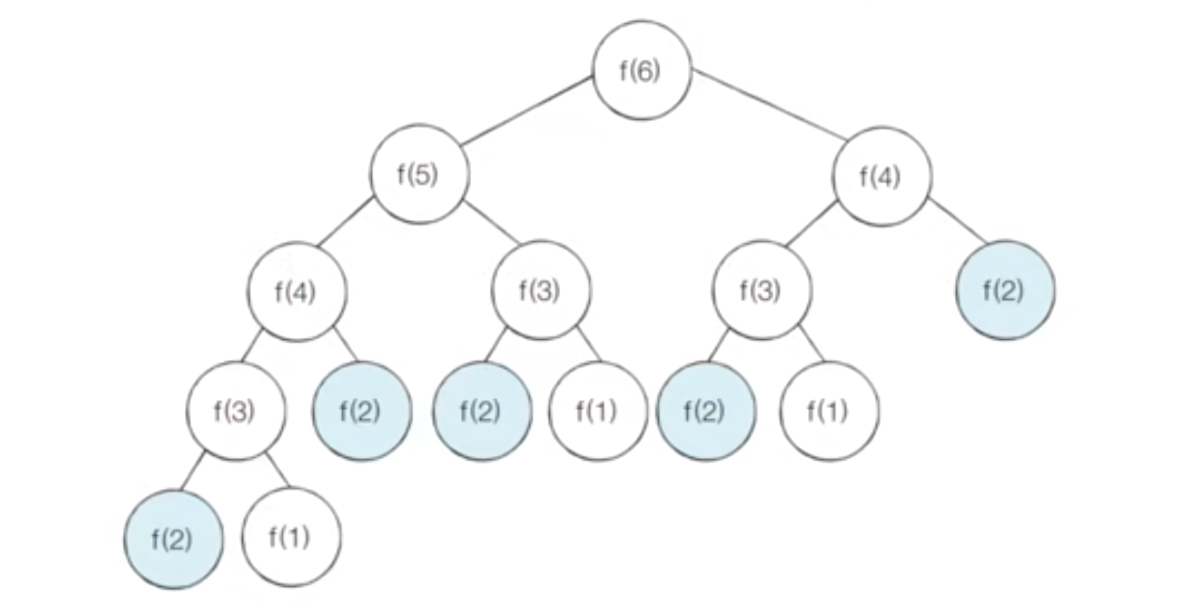
If the already calculated result is memozied in memory, only the colored node is actually called and visited as follows. -> The time complexity is \(O(N)\).
4 Dynamic Programming VS Divide and Conquer
The divide and conquer approach divides a problem into smaller subproblems; these subproblems are further solved recursively. The result of each subproblem is not stored for future reference, whereas, in a dynamic approach, the result of each subproblem is stored for future reference.
Use the divide and conquer approach when the same subproblem is not solved multiple times. Use the dynamic approach when the result of a subproblem is to be used multiple times in the future.
Let us understand this with an example. Suppose we are trying to find the Fibonacci series. Then,
Divide and Conquer approach:
fib(n)
If n < 2, return 1
Else , return f(n - 1) + f(n -2)
Dynamic approach:
mem = []
fib(n)
If n in mem: return mem[n]
else,
If n < 2, f = 1
else , f = f(n - 1) + f(n -2)
mem[n] = f
return f
In a dynamic approach, mem stores the result of each subproblem.
| Dynamic programming | Divide-and-conquer algorithm | |
|---|---|---|
| 1. Optimal Substructure | O | O |
| 2. Overlapping Subproblem | O | X |
Let’s look at a typical example of divide-and-conquer, quick sort.
Once the pivot element changes its position, the position of the pivot element does not change.
The subproblem of re-processing the pivot after splitting is not called.
5 Dynamic Programming Example Problem
5.1 Problem : Ant warrior
The ant warrior secretly attacks the food warehouse of the grasshopper village to make up for the shortage of food. There are several food warehouses in grasshopper Village, which are connected in a straight line.
Each food warehouse stores a fixed number of food, and the ant warriors will selectively plunder the food warehouse to steal food. At this time, the grasshopper scouts can immediately detect when adjacent food warehouses are attacked among the food warehouses that exist in a straight line.
Therefore, in order for the ant warrior to loot the food warehouse without being detected by the scouts, it must loot the food warehouse at least one square away.
For example, suppose there are 4 food depots as follows.
{1, 3, 1, 5}
At this time, the ant warrior can steal a total of 8 food, the maximum value when selecting the second and fourth food warehouses.
The ant warrior wants to get as much food as possible when the food warehouse is in such a straight line.
Write a program to find the maximum amount of food that can be obtained for an ant warrior given information about N food warehouses.
Input conditions
The first line gives the number N of food depots. (3 <=N <=100 )
In the second line, the number K of food stored in each food warehouse is given, based on spaces. (0 <=K <= 1,000)
Output conditions
In the first line, print the maximum amount of food an ant warrior can get.
| Input Example | Output Example |
| 4 | 8 |
| 1 3 1 5 |
5.2 Solution : Ant warrior
Let’s check an example. When N=4, the following cases may exist. The number of food choices is eight as follows. In the 7th case, you get 8 food, so the optimal solution is 8. 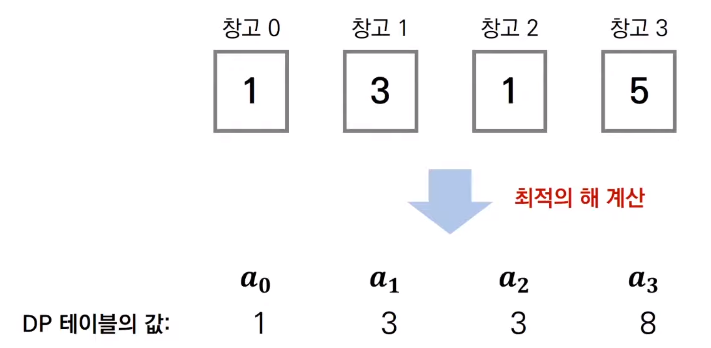
ai = optimal solution to the ith food warehouse (maximum value of food obtainable) If defined in this way, dynamic programming can be applied. Assuming that you turn the food warehouse from left to right, If it is decided whether or not to rob the specific i-th food warehouse, You can choose the one that can steal more food from the two cases below. 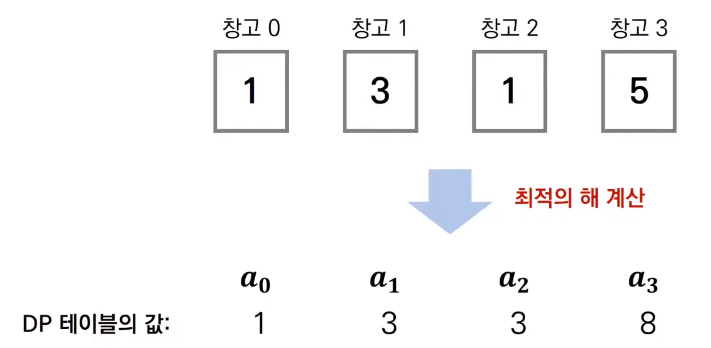
It is decided between the optimal solution up to i-1 and the optimal solution up to i -2 plus the present value. Choose the larger of the two cases. Use 2 small problems to solve the big problems. 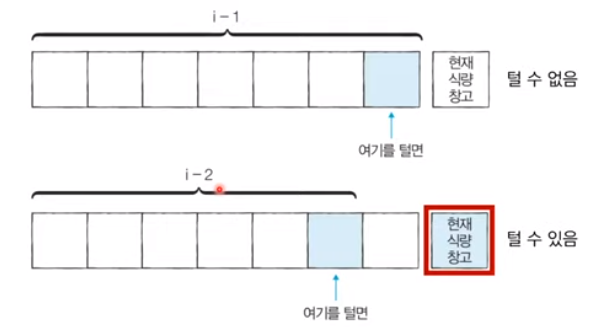
ai = optimal solution to the ith food warehouse (maximum value of food obtainable) ki = amount of food in the ith food pantry The recurrence relation is as follows. ai = max(ai-1, ai-2+ki) Choose the larger of the two Food warehouses more than one square away can always be looted, so there is no need to consider (i-3) and lower.
# title : 'AntWarrior.py'
# Get an integer N
n = int(input( ))
#Get all food information input
array = list(map(int, input( ). split( )))
# Initialize the DP table to save the previously calculated result
d = [0] * 100 #because you can enter up to 100
# Dynamic Programming (Bottom Up)
d[0] = array[0] #maximum value up to first position
d[1] = max( array[0], array[1] ) # Choose the maximum value up to the second position, the larger value
for i in range(2, n); #Optimal solution from position 3 to nth ?
d[i] = max(d[i-1], d[i-2] + array[i] ) # recurrence relation
# Print the calculated result
print(d[n-1])
5.3 Problem : Minimum number of currencies
There are N types of money. We try to minimize the number of these currencies so that the sum of their values is M won. In this case, any number of currencies of each type can be used.
For example, if there are 2 won and 3 won units, using 5 3 won to make 15 won is the minimum number of currencies.
Write a program that prints the minimum number of currencies to make M won.
Input conditions
The first line is given N, M ( 1<= N <=100, 1<= M <= 10,000 )
The next N lines are given the value of each currency. The value of money is a natural number less than or equal to 10,000.
Output conditions
Print the minimum number of currencies on the first line.
If not possible, -1 is output.
| Input Example 1 | Output Example 1 |
| 2 15 | 5 |
| 2 | |
| 3 |
| Input Example 2 | Output Example 2 |
| 3 4 | -1 |
| 3 | |
| 5 | |
| 7 |
5.4 Solution : Minimum number of currencies
\(a_{i}\) = the minimum number of currencies that can make the amount i (the goal is to make the amount M, but solve the small problem first.)
k = unit of each currency
Recurrence relation type: Each currency unit, k, is checked one by one.
- If there is a way to make \(a_{i-k}\), \(a_{i}\) = min(\(a_{i}\), \(a_{i-k+1}\)) is updated with a smaller value.
- If there is no way to create \(a_{i-k}\), \(a_i\) = INF.
Let’s check if N = 3, M = 7, and the units of each currency are 2, 3, 5.
[Step 0]
First, set the value of INF (infinite) to the value corresponding to each index.
INF means that it is not possible to construct a currency that can create a specific amount.
In this problem, 10,001 can be used. 
[Step 1]
Check the first monetary unit, 2. (If you can make i-2, you can also make amount i.) According to the recurrence relation, the list is updated as follows. 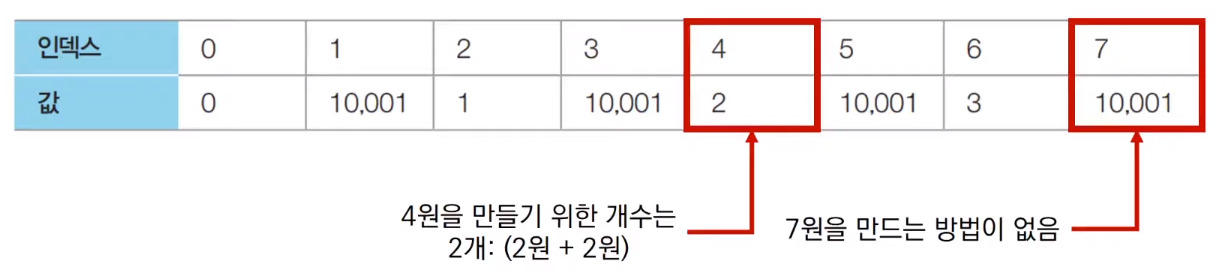
[Step 2]
Check the second monetary unit, 3. According to the recurrence relation, the list is updated as follows. 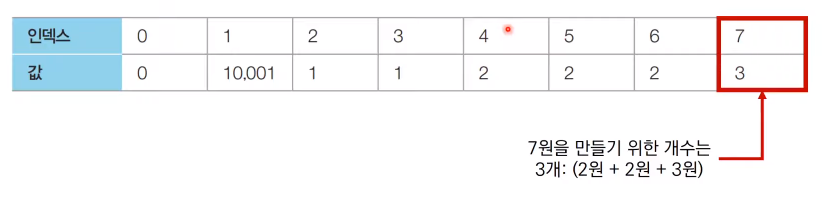
[Step 3]
The third monetary unit, 5, is identified. According to the recurrence relation, the list is finally updated as follows. 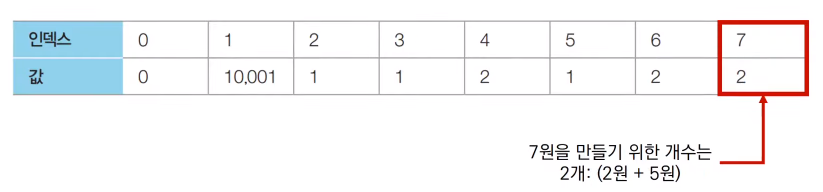
# title : 'MinimumNumberOfCurrencies.py'
# Get score N, M input.
n, m = map(int, input( ). split( ))
# Get information on N currency units.
array = [ ]
for i in range(n):
array.append(int( input( )))
# Initialize the DP table to save the calculated result once.
d = [10001] * (m+1) # We want to find the minimum number of currencies for each amount from 0 won to m won.
# Dynamic Programming (Bottom up)
d[0] =0 # 0 won is the amount that can be made without using anything # i is each currency unit, j is each amount.
for i in range(n): # recurrence relation #for each monetary unit →
for j in range(array[i], m+1): # Check all amounts →
if d[j - array[i]] != 10001: # If there is a way to get the current amount minus the monetary unit = (i-k) won
d[j] = min ( d[j], d[j - array[i] ]+1) # Update the optimal solution for the amount !#Update the smaller value
# Print the calculated result
if d[m] == 10001: # If there is no way to finally create M circle
print(-1)
else: # Print if exists
print(d[m])
5.5 Problem : Gold Mine
There is a gold mine measuring n x m. The gold mine is divided into 1 x 1 squares, each of which contains a certain size of gold.
Miners start with the first row and start digging for gold. You can start from any row in the first column.
After that, it must move to one of three positions: upper right, lower right, and lower right each time over m-1 times.
Write a program that outputs the maximum amount of gold that a miner can obtain as a result.
Input conditions
Test case T is entered in the first line (1<= T <= 1000) Test case: starting number.
In the first line of each test case, n and m are entered separated by spaces. (1<= n,m <= 20)
In the second line, the number of gold buried at n x m locations is entered, separated by spaces. (1 <= number of gold buried at each location <=100)
Output conditions
For each test case, we print the maximum amount of gold that a miner can obtain. Each test case is separated by a line break.
| Input Example | Output Example |
| 2 | 19 |
| 3 4 | 16 |
| 1 3 3 2 2 1 4 1 0 6 4 7 | |
| 4 4 | |
| 1 3 1 5 2 2 4 1 5 0 2 3 0 6 1 2 |
5.6 Solution : Gold Mine
For all locations of gold mines, only the following three things need to be considered.
1. If it comes from the top left.
2. Coming from the lower left.
3. If you are coming from the left.
The problem is solved by updating the table with the case with the most gold among the three cases.
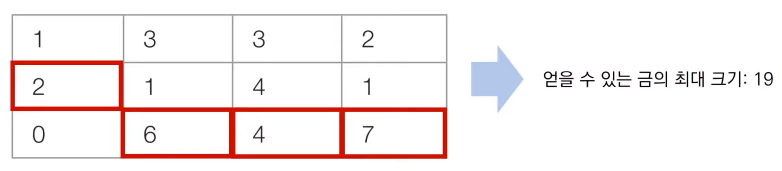
- array[i][j] = amount of gold in row i and column j
- dp[i][j] = best solution to row i and column j (maximum gold value)
The recurrence relation is as follows.
\(dp[i][j] = array[i][j] + max(dp[i-1][j-1], dp[i][j-1], dp[i+1][j-1])\)
#current amount of gold #top-left position #left position #bottom-left position
In this case, whenever you access the table, you need to check whether it is outside the range of the list.
For convenience, there is no need to use a variable array containing initial data.
You can apply dynamic programming by putting the initial data in the DP table.
Check out the process of solving the gold mining problem with dynamic programming.
Initialize the DP table → Put the initial value in the first column → Check the DP table one by one and update the DP table
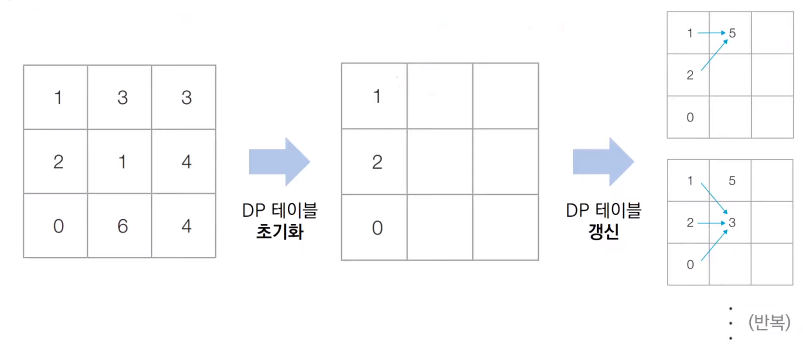
Iteration….the maximum value in the rightmost column is the correct answer required by the problem.
# title : 'GoldMine.py'
for tc in range(int( input( ))):
#Enter gold mine information.
n, m = map(int, input( ). split( ))
array = list(map(int, input( ). split( )))
#Initialize 2D DP table for dynamic programming
dp = [ ]
indx = 0
for i in range(n):
dp. append(array[index: index+m]) Slices in units of # m and puts it in the dp table.
index += m
#Dynamic programming progress (bottom up)
for j in range(1, m): # By column, check each column while moving
for i in range(n):
# If it comes from the top left
if i == 0: left_up = 0 #If out of index, corresponding value=0
else: left_up = dp[ i-1 ][ j-1 ]
#If it comes from the bottom left
if i == n-1: left_down = 0 #If out of index, corresponding value=0
else: left_down = dp[ i+1 ][ j-1 ]
#if coming from the left
left = dp[ i ][ j-1 ]
dp[ i ][ j ] = dp[ i ][ j ] + max( left_up, left_down, left ) #Currently buried gold value + the largest of the three
result = 0
for i in range(n): # Among the values recorded in the rightmost column, ? If you don't understand, check Lesson 6 58:36
result = max( result, dp[ i ][ m-1 ] ) # find the largest value
print( result )
5.7 Problem : Deploying soldiers
N soldiers are randomly listed. Each soldier has a certain value of combat power. When deploying soldiers, we want to arrange them in descending order so that the soldiers with higher combat power are in the front.
In other words, the combat power of the soldier in the front must always be higher than that of the soldier in the back.
Also, in the deployment process, a method of alienating soldiers in a specific position is used.
Still, I want to maximize the number of remaining soldiers.
For example, it is assumed that the combat power of the listed soldiers when N=7 is as follows. 
At this time, if the 3rd and 6th soldiers are excluded, the number of remaining soldiers will be in descending order as follows, and the number will be 5.
This is a way to maximize the number of remaining soldiers. 
Write a program that, given information about soldiers, prints the number of soldiers that must be excluded in order to maximize the number of remaining soldiers.
Input conditions
The first line is given N. (1<= N <=2,000)
In the second line, the combat power of each soldier is given in turn, separated by spaces.
Each soldier’s Combat Strength is a natural number less than or equal to 10,000,000.
Output conditions
The number of soldiers remaining in the first row.
Outputs the number of soldiers that must be excluded to maximize.
5.8 Solution : Deploying soldiers
The basic idea of this problem is the same as that of a classic dynamic programming problem known as Longest Increasing Subsequence (LIS)
For example, let’s say we have a single sequence array = {4, 2, 5, 8, 4, 11, 15}.
The longest increasing subsequence of this sequence is {4, 5, 8, 11, 15}.
Since this problem can be replaced with the problem of finding the longest decreasing subsequence, the correct answer can be derived by applying the LIS algorithm with a slight modification.
Let’s check the longest increasing subsequence (LIS) algorithm.
We define D[i] = the maximum length of a subsequence with array[i] as the last element.
The recurrence relation is as follows.
For all 0 <= j < i , elements i, j
D[i] = max(D[i], D[j]+1 ) Update according to the recurrence relation (the larger of the current value vs. the previous value+1)
if array[j] < array[i] if the preceding element (j) is less than the following element (i) (increasing form) 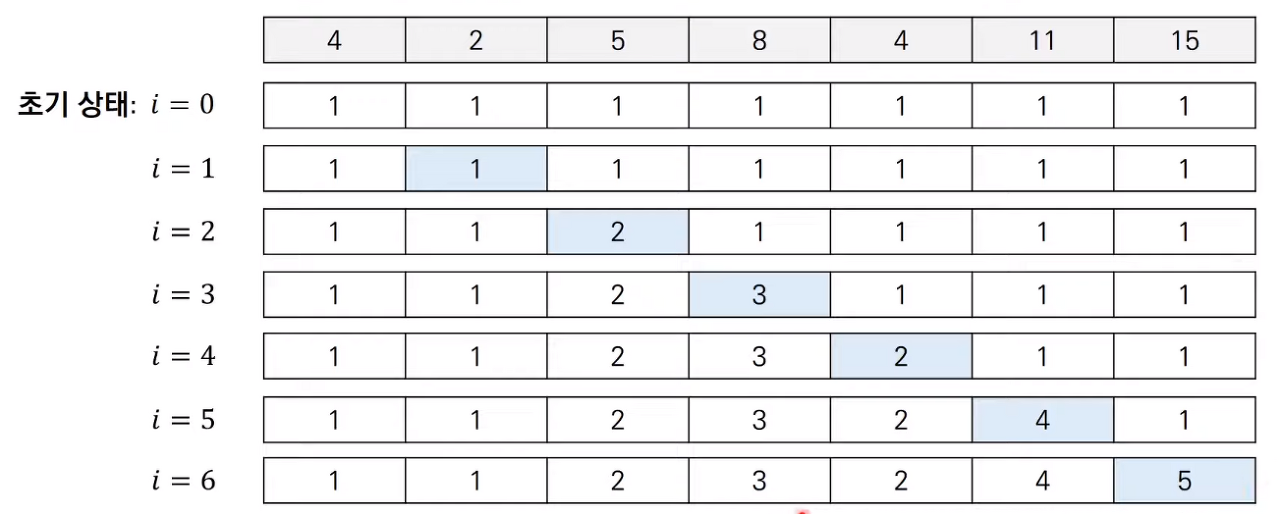
Reverses the order of the soldier information input first.
The correct answer is derived by performing the longest increasing subsequence (LIS) algorithm.
# title : 'DeployingSoldiers.py'
n = int(input( ))
array = list(map(int, input( ).split( )))
# Reverse the order and transform it into a 'longest increasing subsequence' problem
array.reverse( )
#Initialize one-dimensional DP table for dynamic programming
dp = [1] * n
#Perform the longest increasing subsequence (LIS) algorithm
for i in range(1, n): #from the second element to the last element
for j in range(0, i): #All elements before (j) = from the first element to before i
if array[ j ] < array[ i ]: #only if small
dp[ i ] = max( dp[ i ], dp[ j ]+1 ) # recurrence relation
# Print the minimum number of soldiers to be excluded
print(n - max(dp)) # Subtract the value from all n
https://www.freecodecamp.org/
https://www.programiz.com/
https://www.geeksforgeeks.org/
https://blog.naver.com/PostList.naver?blogId=ndb796
이것이 코딩테스트다,2020,나동빈,한빛미디어