DFS & BFS
The Pine Tree at Saint-Tropez, 1909, Paul Signac
Search is the process of finding the desired data among a large amount of data.
1. DFS (Depth-First Search)
1.1 What is DFS?
DFS is a depth-first search algorithm that preferentially searches the deep part of a graph.
DFS uses a stack data structure(or a recursive function), and the detailed operation process is as follows.
- Insert the search start node into the stack set it visited.
- If there is at least one unvisited adjacent node at the top node of the stack, the node is put into the stack and set visited. If there are no unvisited adjacent nodes, the top node is popped off the stack.
- Repeat until Step 2 can no longer be performed.
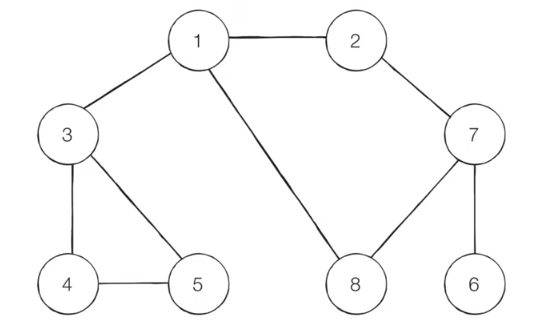
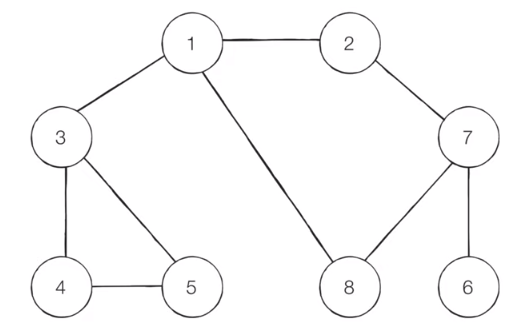
[Step 0]
Prepare the graph. (visit criteria: starting with the lowest adjacent nodes)
- Start Node: 1
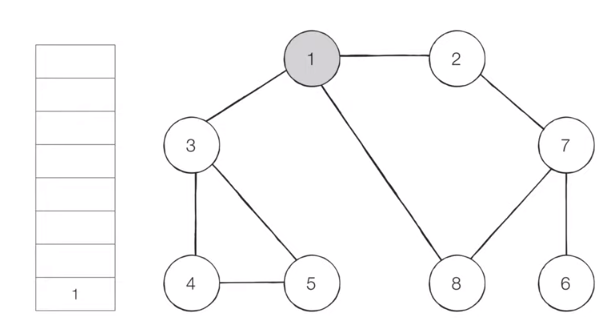
[Step 1]
Insert the starting node ‘1’ into the stack and set it visited.
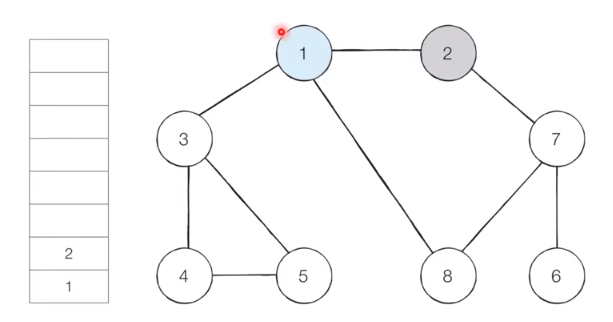
[Step 2]
There are unvisited adjacent nodes 2, 3, and 8 at ‘1’, which is the top node of the stack. Among them, 2, the smallest node, is put on the stack and set visited.
[Step 3]
There is an unvisited adjacent node 7 at the top node 2 of the stack. Therefore, we put node 7 on the stack and set visited.
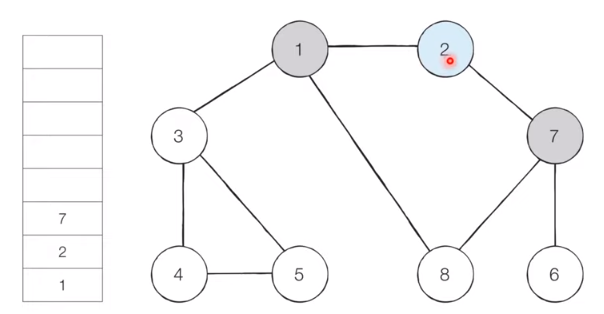
[Step 4]
There are unvisited adjacent nodes 6 and 8 in 7, which is the top node of the stack. Among them, 6, the smallest node, is put on the stack and set visited.
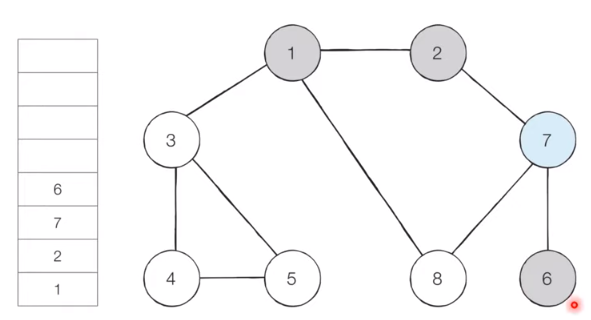
[Step 5]
The top node of the stack, ‘6’, has no unvisited adjacent nodes. Therefore, we pop node ‘6’ from the stack.
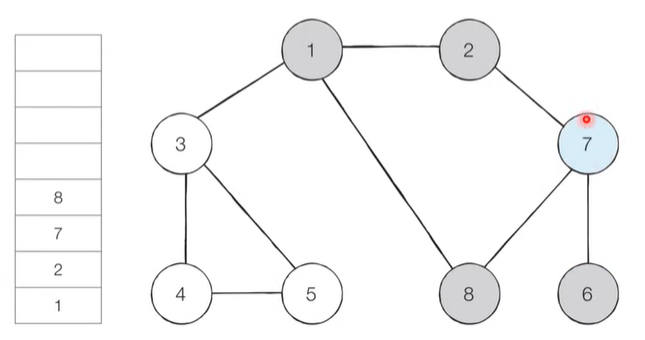
[Step 6]
The top node of the stack, ‘7’, has an unvisited neighbor ‘8’. Therefore, we put node ‘8’ on the stack and set visited.
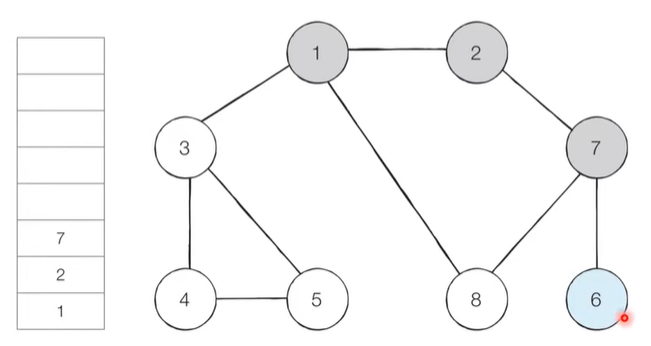
Navigation order: 1 -> 2 -> 7 -> 6 -> 8 -> 3 -> 4 -> 5
1.2 DFS Implementation
# file:'DFS.py'
# Define the BFS method
def dfs(graph, v, visited): # Use the list of graph information and visited processing.
# Set the current node visited
visited[v] = True
print(v, end=' ')
# Recursively visit other nodes connected to the current node
for i in graph[v]:
if not visited[i]: # If not visited
dfs(graph, i, visited) # Set visited using recursive function
# Represents information connected to each node (2D list)
graph = [
[], # Leave the part with index 0 blank.
[2, 3, 8], # nodes adjacent to node '1'
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
# Represents each node visited information (one-dimensional list)
visited = [False] * 9 # Initially treat all nodes as never visited.
# In order not to use index 0, initialize the list with n+1 number 9. It's more intuitive.
# Call the defined DFS function
dfs(graph, 1, visited)
# Output
# 1 2 7 6 8 3 4 5
2. BFS (Breadth-First Search)
2.1 What is BFS?
BFS is a breadth-first search algorithm that searches first from the nearest node in the graph.
BFS uses a queue data structure, and the detailed operation process is as follows.
- Insert the search start node into the queue and set visited.
- After removing a node from the queue, all unvisited nodes among the nodes adjacent to the node are inserted into the queue and set visited.
- Repeat until Step 2 can no longer be performed.
BFS is effective for shortest path troubleshooting purposes under certain conditions.
[Step 0]
Prepare the graph. (visit criteria: starting with the lowest adjacent nodes)
- Start Node: 1
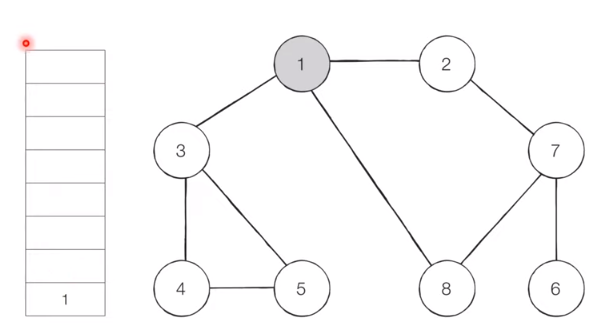
[Step 1]
Insert 1, the starting node, into the queue and set visited.
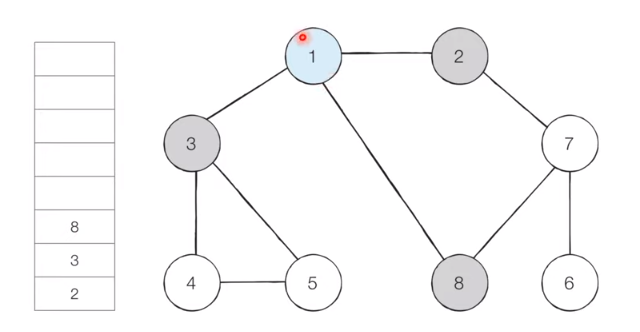
[Step 2]
Remove node 1 from the queue, insert unvisited adjacent nodes 2, 3, and 8 into the queue and set visited.
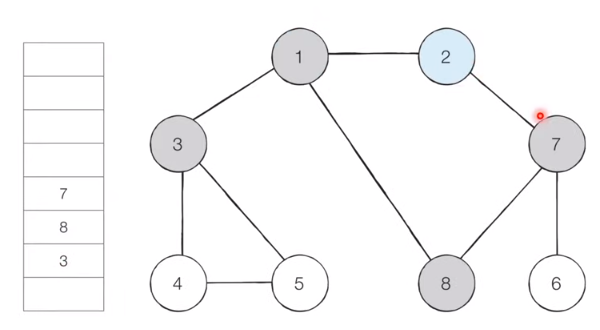
[Step 3]
Remove node 2 from the queue, insert unvisited adjacent node 7 into the queue, and set visited.(1 is visited nodes.)
[Step 4]
Remove node 3 from the queue, insert unvisited adjacent nodes 4 and 5 into the queue, and set visited.
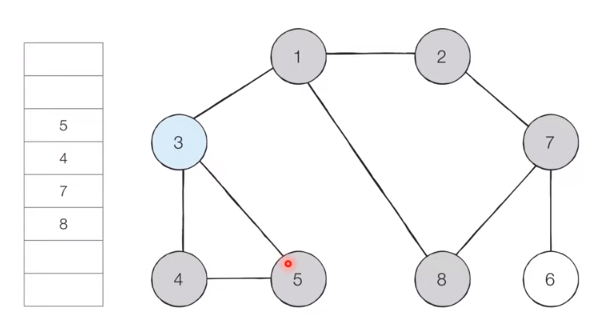
[Step 5]
Remove node 8 from the queue and ignore it as there are no unvisited adjacent nodes.
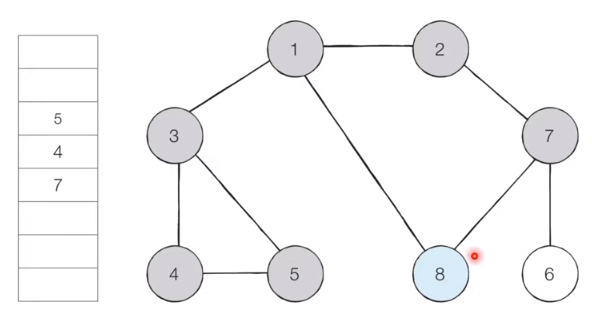
Navigation order: 1 -> 2 -> 3 -> 8 -> 7 -> 4 -> 5 -> 6
It can be used to solve the shortest distance problem in a situation where the cost of each edge is the same.
2.2 BFS Implementation
# file:'BFS.py'
from collections import deque
# Define the BFS method
def bfs(graph, start, visited):
#Use deque library to implement queue
queue = deque([start]) #Put the starting node into the queue.
# Visit the current node
visited[start] = True
# Repeat until the queue is empty
while queue:
# Pull an element from the queue and print it
v = queue .popleft() #popleft() : Fetches the element that came in first.
print(v, end=' ')
# Insert adjacent elements that have not yet been visited into the queue
for i in graph[v]:
if not visited[i]:
queue.append(i)
visited[i] = True
# Represents information connected to each node (2D list)
graph = [
[], # Creates a list object with 9 elements. 0 index is empty.
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
# Represents each node visited information (one-dimensional list)
visited = [False] * 9
# Call the defined BFS function
bfs(graph, 1, visited)
# Output
# 1 2 3 8 7 4 5 6
3. DFS & BFS Example Problem
3.1 Problem : Freezing drinks
There is an ice frame of size N X M. Areas with holes are marked with 0, and areas with partitions are marked with 1.
If the parts with holes are attached to each other in the top, bottom, left, and right directions, it is considered to be connected to each other.
At this time, write a program to find the total number of ice creams generated when the shape of the ice mold is given.
In the following 4 X 5 ice mold example, a total of 3 ice creams are created.

Finding a connected element, connected_component is also a problem.
Input conditions
The first line gives the vertical length N and the horizontal length M of the ice frame. (1 <= N, M <= 1,000) Total ice frame space: 1 million or less.
From the second row to the N+1 row, the shape of the ice frame is given.
In this case, the open part is 0, and the closed part is 1.
Output conditions
Prints the number of ice creams that can be made at one time.
3.2 Solution : Freezing drinks
This problem can be solved with DFS or BFS. It is modeled in the form of a graph because it expresses that the ice space is connected to the top, bottom, left, and right. If the count is performed only for the point where the visit processing is performed, the total number of connected elements can be calculated. The algorithm using DFS is as follows.
- After examining the top, bottom, left, and right around a specific point, If there is a point that has not yet been visited with a value of 0 among nearby points, the corresponding point is visited.
- If you repeat the process of visiting while looking up, down, left, and right at the visited point, you can visit all the connected points.
- Repeat Steps 1 and 2 for all nodes, and count the number of unvisited points.
# title: 'FreezingDrinks.py'
# Visit a specific node with DFS and visit all connected nodes
def dfs(x, y):
# Exit immediately if outside the given range
if x <= -1 or x >= n or y <= -1 or y <= m:
return False
# if the current node has not been visited yet
if graph[x][y] == 0:
# Process the node visit
graph[x][y] = 1
# Top, bottom, left, and right positions are all called recursively
dfs( x-1, y )
dfs( x, y-1 )
dfs( x+1, y )
dfs( x, y+1 )
return True #Enables returning True value as a result. It counts because dfs has been performed at the current location.
return False
# Get input by separating N and M by space
n, m = map(int, input() . split())
#Get map information of 2D list
graph = [ ]
for i in range(n):
graph .append(list(map(int, input()))) # Takes a single line, converts it to an integer type, and converts it back to a list type
#Fill drinks for all nodes (positions)
result = 0
for i in range(n):
for j in range(m):
# Do DFS in place
if dfs(i, j) == True: #if the visit has been processed
result += 1 # count at that time.
print(result) #print the correct answer
3.3 Problem : Maze Escape
Chan was trapped in a maze in the shape of a rectangle of size N X M. There are several monsters in the maze, and chan have to escape from them.
The position of chan is (1, 1) and the exit of the maze is at the position of (N, M), and it can move one space at a time. In this case, the area with monsters is marked with 0, and the area without monsters is marked with 1. The maze comes out in a form that must be escaped.
At this time, find the minimum number of squares that chan must move to escape. When counting cells, both the start cell and the end cell are counted.
Input conditions
The first line gives two integers N, M(4 <= N, M <= 200).
In each of the next N lines, M number of integers (0 or 1) are given the information of the maze. Each number is presented as input, concatenated without spaces. The first and last cells are always 1.
Output conditions
Print the minimum number of moving cells on the first line.
3.4 Solution : Maze Escape
BFS searches all the nodes in the graph in order, starting with the node closest to the starting point.
The distance to all nodes connected to the top, bottom, left, and right is equal to 1.
Therefore, it can be solved by performing BFS from the point (1, 1) and recording the shortest distance values of all nodes.
[Step 1]
Start at position (1, 1).
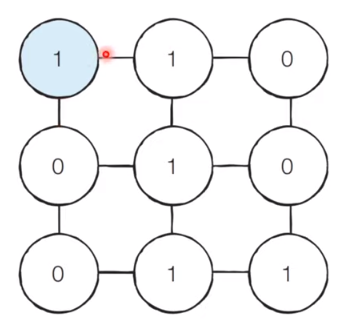
[Step 2]
If you search up, down, left, and right from the (1, 1) coordinates, you will visit the node at the (1, 2) position, which is the next node, the value of the newly visited (1, 2) node is changed to 2.
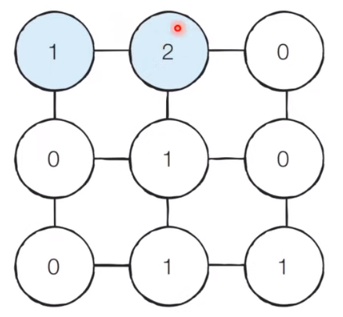
Reason: Distance is 2. This is because the shortest path must be recorded. This node will also be queued. After taking this node out again, it searches up, down, left and right, and then visits the adjacent node. Each time you visit a new point, add +1 distance to the previous point.
[Step 3]
Similarly, if BFS is continuously performed, as a result, the values of the shortest path are changed to increase by one as follows.
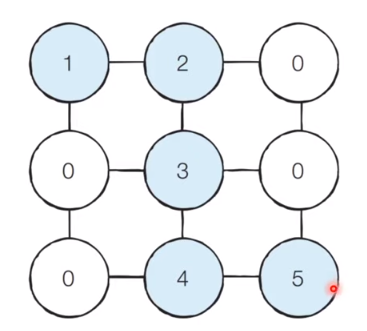
# title: 'MazeEscape.py'
def bfs(x, y):
# Use deque library to implement queue
queue = deque()
queue.append((x, y)) # Contains tuple data of (x, y).
# Repeat until queue is empty
while queue:
x, y = queue. popleft() # Take an element from the queue on each iteration
# Check the location in 4 directions from the current location
for i in range(4):
nx = x+dx[i]
ny = y+dy[i]
# Ignore if out of maze find space
if nx < 0 or nx >=n or ny < 0 or ny >= m:
continue
# Ignore if it is a wall (monster)
if graph[nx][ny] == 0:
continue
# Record the shortest distance only when the node is visited for the first time
if graph[nx][ny] == 1:
graph[nx][ny] = graph[x][y] + 1 # Add 1 to the value of the previous node.
queue .append((nx, ny))
# Returns the shortest distance to the bottom right
return graph[n-1][m-1]
from collections import deque
# Get input by separating N and M by a space
n, m = map(int, input(). split())
# Get map information of 2D list
graph = []
for i in range(n):
graph.append(list(map(int, input())))
# Define four directions to move (up, down, left, right).
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
# Output the result of performing BFS
print(bfs(0, 0))
https://www.freecodecamp.org/
https://www.programiz.com/
https://www.geeksforgeeks.org/
https://blog.naver.com/PostList.naver?blogId=ndb796
이것이 코딩테스트다,2020,나동빈,한빛미디어