Longest Subsequence

Avant Port De Dieppe, circa 1928-1929, Gustave Loiseau
- 1. Longest Increasing Subsequence
- 2. Longest Common Subsequence
- 3. Longest Common Increasing Subsequence (LCS + LIS)
1. Longest Increasing Subsequence
1.1 What is LIS?
The Longest Increasing Subsequence (LIS) problem is to find the length of the longest subsequence of a given sequence such that all elements of the subsequence are sorted in increasing order. For example, the length of LIS for {10, 22, 9, 33, 21, 50, 41, 60, 80} is 6 and LIS is {10, 22, 33, 50, 60, 80}.

Examples:
Input: arr[] = {3, 10, 2, 1, 20}
Output: Length of LIS = 3
The longest increasing subsequence is 3, 10, 20
Input: arr[] = {3, 2}
Output: Length of LIS = 1
The longest increasing subsequences are {3} and {2}
Input: arr[] = {50, 3, 10, 7, 40, 80}
Output: Length of LIS = 4
The longest increasing subsequence is {3, 7, 40, 80}
1.2 Dynamic Programming based solution
This problem has Obtimal Substructure property and Overlapping Subproblem.It can be avoided by either using Memoization or Tabulation. => Dynamic Programming
The simulation of approach will make things clear:
Input : arr[] = {3, 10, 2, 11}
LIS[] = {1, 1, 1, 1} (initially)
Iteration-wise simulation :
arr[0] < arr[1] {TEMP = LIS[0], LIS[1] = LIS[1] + TEMP = 2}
arr[0] > arr[2] {No change}
arr[1] > arr[2] {No change}
arr[0] < arr[3] {TEMP = LIS[0]}
arr[1] < arr[3] {TEMP = max(TEMP, LIS[1]) = 2}
arr[2] < arr[3] {TEMP = max(TEMP, LIS[2]) = 3, LIS[3] = LIS[3] + TEMP}
We can avoid recomputation of subproblems by using tabulation as shown in the below code:
# title: 'LIS.py'
# lis returns length of the longest increasing subsequence in arr of size n
def lis(arr):
n = len(arr)
# Declare the list (array) for LIS and initialize LIS values for all indexes
lis = [1]*n
# Compute optimized LIS values in bottom up manner
for i in range(1, n):
temp_max = 0
for j in range(0, i):
if arr[j] < arr[i] and temp_max < lis[j]:
temp_max = lis[j]
lis[i] = lis[i] + temp_max
# Initialize maximum to 0 to get the maximum of all LIS
maximum = 0
# Pick maximum of all LIS values
for i in range(n):
maximum = max(maximum, lis[i])
return maximum
# end of lis function
# Driver program to test above function
arr = [10, 22, 9, 33, 21, 50, 41, 60]
print ("Length of lis is", lis(arr))
# Output
# Length of lis is 5
1.3 Time Complexity
Time Complexity: \(O(n^2)\).
- As nested loop is used.
Auxiliary Space: \(O(n)\).
- Use of any array to store LIS values at each index.
The time complexity of the above Dynamic Programming (DP) solution is \(O(n^2)\) and there is a \(O(NlogN)\) solution for the LIS problem. See below link for the solution.
Longest Increasing Subsequence (\(\underline{NlogN}\))
2. Longest Common Subsequence
2.1 What is LCS?
The Longest Common Subsequence (LCS) is defined as the longest subsequence that is common to all the given sequences, provided that the elements of the subsequence are not required to occupy consecutive positions within the original sequences.
If S1 and S2 are the two given sequences then, Z is the common subsequence of S1 and S2 if Z is a subsequence of both S1 and S2. Furthermore, Z must be a strictly increasing sequence of the indices of both S1 and S2.
In a strictly increasing sequence, the indices of the elements chosen from the original sequences must be in ascending order in Z.
If
S1 = {B, C, D, A, A, C, D}
Then, {A, D, B} cannot be a subsequence of S1 as the order of the elements is not the same (ie. not strictly increasing sequence).
If
S1 = {B, C, D, A, A, C, D}
S2 = {A, C, D, B, A, C}
Then, common subsequences are {B, C}, {C, D, A, C}, {D, A, C}, {A, A, C}, {A, C}, {C, D}, ... Among these subsequences, {C, D, A, C} is the longest common subsequence. We are going to find this longest common subsequence using dynamic programming.
2.2 Dynamic Programming based solution
Let us take two sequences:

The first sequence
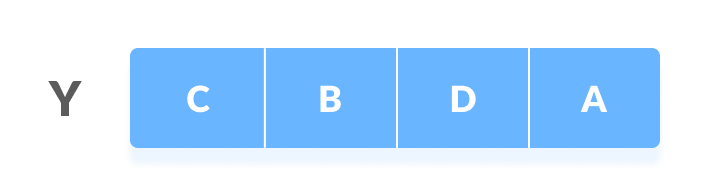
Second Sequence
The following steps are followed for finding the longest common subsequence.
[Step 1]
Create a table of dimension n+1*m+1 where n and m are the lengths of X and Y respectively. The first row and the first column are filled with zeros.
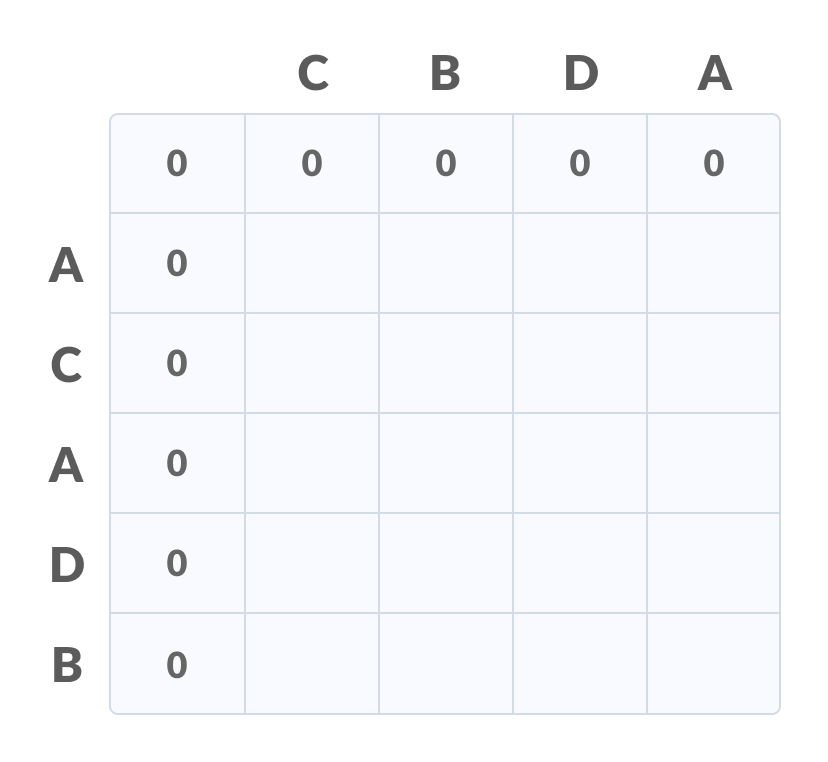
Initialise a table
[Step 2]
Fill each cell of the table using the following logic.
If the character correspoding to the current row and current column are matching, then fill the current cell by adding one to the diagonal element. Point an arrow to the diagonal cell.
Else take the maximum value from the previous column and previous row element for filling the current cell. Point an arrow to the cell with maximum value. If they are equal, point to any of them.
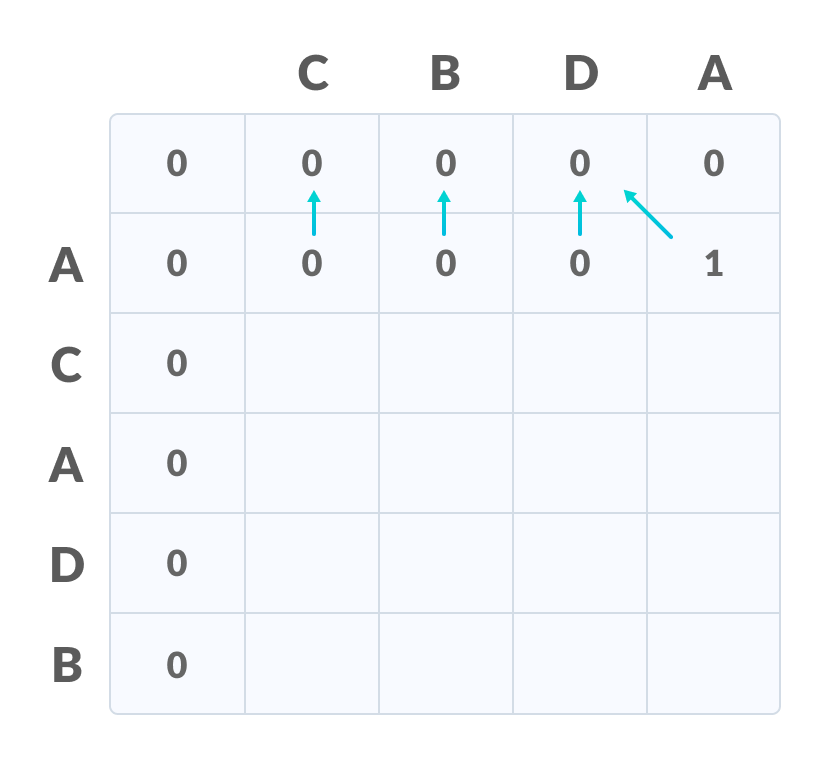
Fill the values
[Step 3]
Step 2 is repeated until the table is filled.
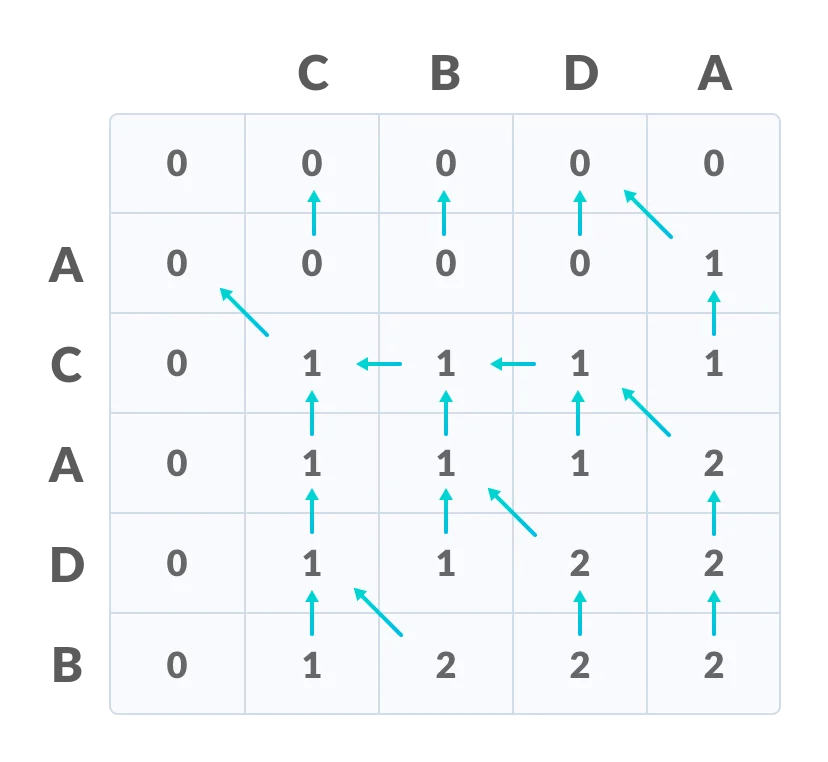
Fill the values
[Step 4]
The value in the last row and the last column is the length of the longest common subsequence.
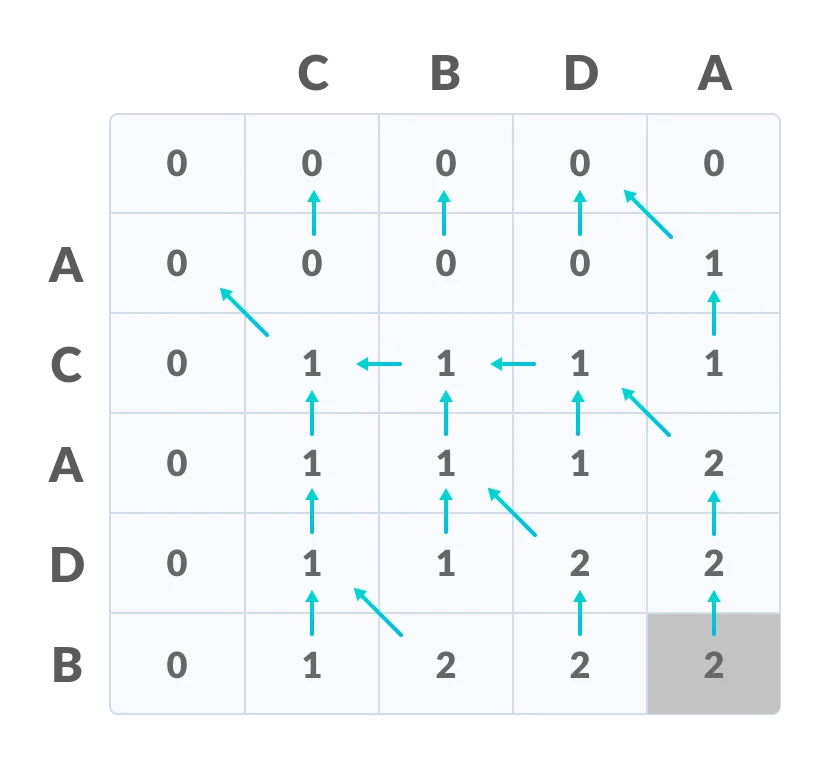
The bottom right corner is the length of the LCS
[Step 5]
In order to find the longest common subsequence, start from the last element and follow the direction of the arrow. The elements corresponding to () symbol form the longest common subsequence.
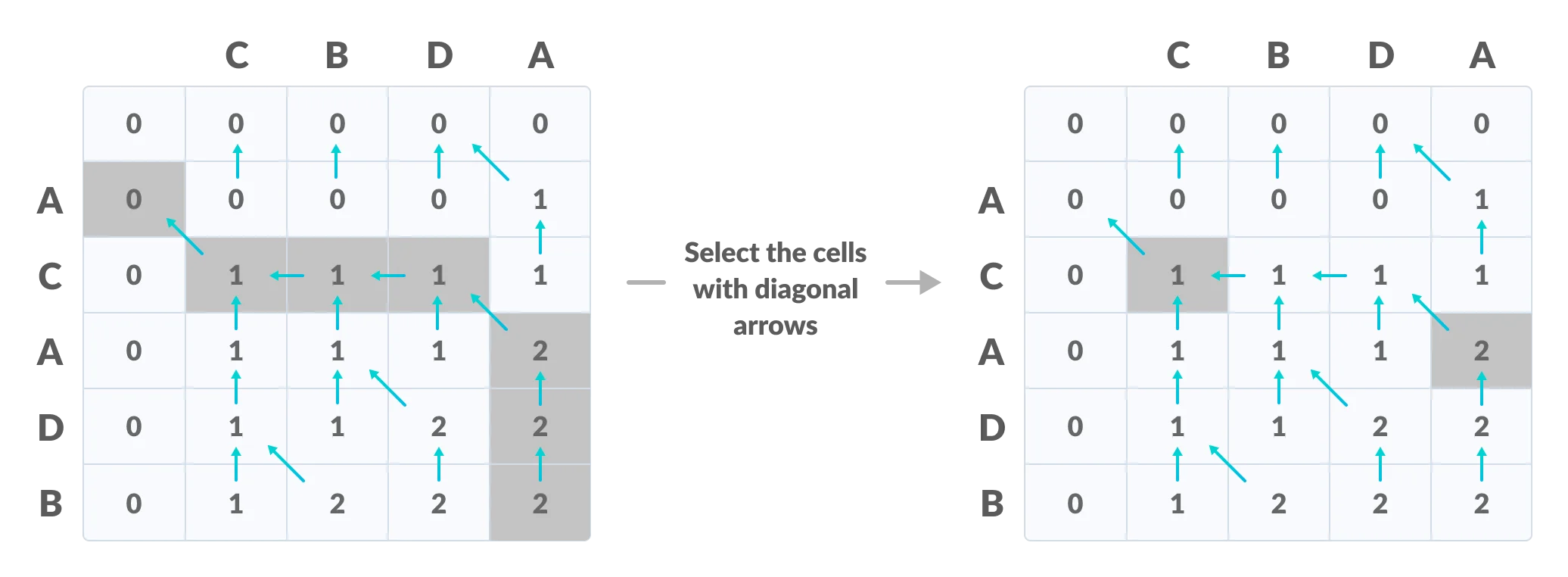
Create a path according to the arrows
Thus, the longest common subsequence is CA.

LCS
Longest Common Subsequence Algorithm
X and Y be two given sequences
Initialize a table LCS of dimension X.length * Y.length
X.label = X
Y.label = Y
LCS[0][] = 0
LCS[][0] = 0
Start from LCS[1][1]
Compare X[i] and Y[j]
If X[i] = Y[j]
LCS[i][j] = 1 + LCS[i-1, j-1]
Point an arrow to LCS[i][j]
Else
LCS[i][j] = max(LCS[i-1][j], LCS[i][j-1])
Point an arrow to max(LCS[i-1][j], LCS[i][j-1])
# title: 'LCS.py'
# Function to find lcs_algo
def lcs(X, Y):
# find the length of the strings
m = len(X)
n = len(Y)
# declaring the array for storing the dp values
L = [[None]*(n+1) for i in range(m+1)]
"""Following steps build L[m+1][n+1] in bottom up fashion
Note: L[i][j] contains length of LCS of X[0..i-1] and Y[0..j-1]"""
for i in range(m+1):
for j in range(n+1):
if i == 0 or j == 0 :
L[i][j] = 0
elif X[i-1] == Y[j-1]:
L[i][j] = L[i-1][j-1]+1
else:
L[i][j] = max(L[i-1][j] , L[i][j-1])
# L[m][n] contains the length of LCS of X[0..n-1] & Y[0..m-1]
return L[m][n]
#end of function lcs
# Driver program to test the above function
X = "AGGTAB"
Y = "GXTXAYB"
print ("Length of LCS is ", lcs(X, Y) )
Longest Common Subsequence Applications
in compressing genome resequencing data to authenticate users within their mobile phone through in-air signatures
1.3 Time Complexity
Time Complexity: \(O(mn)\)
The method of dynamic programming reduces the number of function calls. It stores the result of each function call so that it can be used in future calls without the need for redundant calls.
In the above dynamic algorithm, the results obtained from each comparison between elements of X and the elements of Y are stored in a table so that they can be used in future computations.
So, the time taken by a dynamic approach is the time taken to fill the table (ie. \(O(mn)\)). Whereas, the recursion algorithm has the complexity of \(2max(m, n)\).
3. Longest Common Increasing Subsequence (LCS + LIS)
Given two arrays, find length of the longest common increasing subsequence [LCIS] and print one of such sequences (multiple sequences may exist)
Suppose we consider two arrays –
arr1[] = {3, 4, 9, 1}
arr2[] = {5, 3, 8, 9, 10, 2, 1}
Our answer would be {3, 9} as this is the longest common subsequence which is increasing also.
The idea is to use dynamic programming here as well. We store the longest common increasing sub-sequence ending at each index of arr2[]. We create an auxiliary array table[] such that table[j] stores length of LCIS ending with arr2[j]. At the end, we return maximum value from this table. For filling values in this table, we traverse all elements of arr1[] and for every element arr1[i], we traverse all elements of arr2[]. If we find a match, we update table[j] with length of current LCIS. To maintain current LCIS, we keep checking valid table[j] values.
Below is the program to find length of LCIS.
# title: 'LCIS.py'
# Returns the length and the LCIS of two arrays arr1[0..n-1] and arr2[0..m-1]
def LCIS(arr1, n, arr2, m):
# table[j] is going to store length of LCIS
# ending with arr2[j]. We initialize it as 0,
table = [0] * m
for j in range(m):
table[j] = 0
# Traverse all elements of arr1[]
for i in range(n):
# Initialize current length of LCIS
current = 0
# For each element of arr1[], traverse all elements of arr2[].
for j in range(m):
# If both the array have same elements.
# Note that we don't break the loop here.
if (arr1[i] == arr2[j]):
if (current + 1 > table[j]):
table[j] = current + 1
# Now seek for previous smaller common element for current element of arr1
if (arr1[i] > arr2[j]):
if (table[j] > current):
current = table[j]
# The maximum value in table[] is out result
result = 0
for i in range(m):
if (table[i] > result):
result = table[i]
return result
# Driver Code
if __name__ == "__main__":
arr1 = [3, 4, 9, 1]
arr2 = [5, 3, 8, 9, 10, 2, 1]
n = len(arr1)
m = len(arr2)
print("Length of LCIS is",
LCIS(arr1, n, arr2, m))
# Output :
# Length of LCIS is 2