Largest Rectangular Area in a Histogram
Le potager en hiver, 1921, Gustave Loiseau
Find the largest rectangular area possible in a given histogram where the largest rectangle can be made of a number of contiguous bars.
1. Divide and Conquer based solution
For simplicity, assume that all bars have same width and the width is 1 unit.
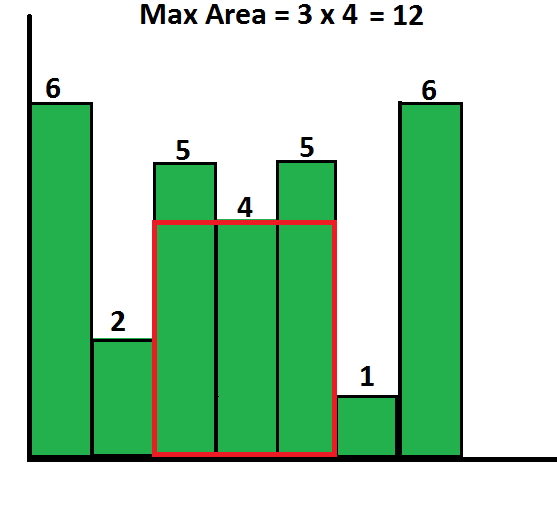
For example, consider the following histogram with 7 bars of heights {6, 2, 5, 4, 5, 1, 6}. The largest rectangle possible is 12 (see the below figure).
A simple solution is to one by one consider all bars as starting points and calculate area of all rectangles starting with every bar. Finally return maximum of all possible areas. Time complexity of this solution would be \(O(n^2).\)
We can use Divide and Conquer to solve this in \(O(nlogn)\) time. The idea is to find the minimum value in the given array. Once we have index of the minimum value, the max area is maximum of following three values.
a) Maximum area in left side of minimum value (Not including the min value)
b) Maximum area in right side of minimum value (Not including the min value)
c) Number of bars multiplied by minimum value.
The areas in left and right of minimum value bar can be calculated recursively. If we use linear search to find the minimum value, then the worst case time complexity of this algorithm becomes \(O(n^2)\). In worst case, we always have (n-1) elements in one side and 0 elements in other side and if the finding minimum takes \(O(n)\) time, we get the recurrence similar to worst case of Quick Sort.
To find the minimum efficiently, Range Minimum Query using Segment Tree can be used for this. We build segment tree of the given histogram heights. Once the segment tree is built, all range minimum queries take \(O(logn)\) time. So over all complexity of the algorithm becomes.
Overall Time = Time to build Segment Tree + Time to recursively find maximum area Time to build segment tree is \(O(n)\). Let the time to recursively find max area be T(n). It can be written as following.
\(T(n)\) = \(O(logn)\) + \(T(n-1)\)
The solution of above recurrence is \(O(nlogn)\). So overall time is \(O(n)\) + \(O(nlogn)\) which is \(\underline{O(nlogn)}\).
# title: LargestRectangularAreainaHistogram1.py
# query using segment tree
# modified to return index of minimum instead of minimum itself
#-------------------------------------------------------------------------
from math import ceil,log2;
# A utility function to get minimum of two numbers
def minVal(hist,x, y) :
if x==-1:
return y
if y==-1:
return x
return x if (hist[x] < hist[y]) else y;
# A utility function to get the middle index from corner indexes.
def getMid(s, e) :
return s + (e - s) // 2;
""" A recursive function to get the minimum value in a given range
of array indexes. The following are parameters for this function.
st --> Pointer to segment tree
index --> Index of current node in the segment tree. Initially 0 is passed as root is always at index 0
ss & se --> Starting and ending indexes of the segment represented by current node, i.e., st[index]
qs & qe --> Starting and ending indexes of query range """
def RMQUtil( hist,st, ss, se, qs, qe, index) :
# If segment of this node is a part of given range, then return the min of the segment
if (qs <= ss and qe >= se) :
return st[index];
# If segment of this node is outside the given range
if (se < qs or ss > qe) :
return -1;
# If a part of this segment overlaps with the given range
mid = getMid(ss, se);
return minVal(hist,RMQUtil(hist,st, ss, mid, qs, qe, 2 * index + 1),
RMQUtil(hist,st, mid + 1, se, qs, qe, 2 * index + 2));
# Return minimum of elements in range from index qs (query start) to qe (query end).
# It mainly uses RMQUtil()
def RMQ( hist,st, n, qs, qe) :
# Check for erroneous input values
if (qs < 0 or qe > n - 1 or qs > qe) :
print("Invalid Input");
return -1;
return RMQUtil(hist,st, 0, n - 1, qs, qe, 0);
# A recursive function that constructs Segment Tree for array[ss..se].
# si is index of current node in segment tree st
def constructSTUtil(hist, ss, se, st, si) :
# If there is one element in array, store it in current node of segment tree and return
if (ss == se) :
st[si] = ss;
return st[si];
# If there are more than one elements, then recur for left and right subtrees
# and store the minimum of two values in this node
mid = getMid(ss, se);
st[si] = minVal(hist,constructSTUtil(hist, ss, mid, st, si * 2 + 1),
constructSTUtil(hist, mid + 1, se, st, si * 2 + 2));
return st[si];
"""Function to construct segment tree from given array. This function allocates
memory for segment tree and calls constructSTUtil() to fill the allocated memory """
def constructST( hist, n) :
# Allocate memory for segment tree
# Height of segment tree
x = (int)(ceil(log2(n)));
# Maximum size of segment tree
max_size = 2 * (int)(2**x) - 1;
st = [0] * (max_size);
# Fill the allocated memory st
constructSTUtil(hist, 0, n - 1, st, 0);
# Return the constructed segment tree
return st;
#----------------------------------------------------------------
# main program
# using Divide and Conquer to find maximum rectangular area under a histogram
def max_area_histogram(hist):
area=0
#initialize area
st = constructST(hist, len(hist))
# construct the segment tree
try:
# try except block is generally used in this way to suppress all type of exceptions raised.
def fun(left,right):
# this function "fun" calculates area recursively between indices left and right
nonlocal area
# global area won't work here as variable area is defined inside function not in main().
if left==right:
return
# the recursion has reached end
index = RMQ(hist,st, len(hist), left, right-1)
# RMQ function returns index of minimum value in the range of [left,right-1]
# can also be found by using min() but results in O(n) instead of O(log n) for traversing
area=max(area,hist[index]*(right-left))
# calculate area with minimum above
fun(index+1,right)
fun(left,index)
# initiate further recursion
return
# initializes the recursion
fun(0,len(hist))
# return the max area to calling function in this case "print"
return(area)
except:
pass
# Driver Code
hist = [6, 2, 5, 4, 5, 1, 6]
print("Maximum area is",
max_area_histogram(hist))
2. More efficient(\(O(n)\)) solution
2.1 Solution 1
Divide and conquer based solution has the time complexity of \(O(nlogn)\), but there is a way to reduce it to \(\underline{O(n)}\).
- For every bar ‘x’, we calculate the area with ‘x’ as the smallest bar in the rectangle.
- If we calculate such area for every bar ‘x’ and find the maximum of all areas, our task is done.
To calculate area with ‘x’ as smallest bar, need to know index of the first smaller (smaller than ‘x’) bar on left of ‘x’ and index of first smaller bar on right of ‘x’. Let us call these indexes as ‘left index’ and ‘right index’ respectively.
We traverse all bars from left to right, maintain a stack of bars. Every bar is pushed to stack once. A bar is popped from stack when a bar of smaller height is seen. When a bar is popped, we calculate the area with the popped bar as smallest bar. How do we get left and right indexes of the popped bar – the current index tells us the ‘right index’ and index of previous item in stack is the ‘left index’.
Following is the complete algorithm.
1) Create an empty stack.
2) Start from first bar, and do following for every bar ‘hist[i]’ where ‘i’ varies from 0 to n-1.
……a) If stack is empty or hist[i] is higher than the bar at top of stack, then push ‘i’ to stack.
……b) If this bar is smaller than the top of stack, then keep removing the top of stack while top of the stack is greater.
Let the removed bar be hist[tp]. Calculate area of rectangle with hist[tp] as smallest bar.
For hist[tp], the ‘left index’ is previous (previous to tp) item in stack and ‘right index’ is ‘i’ (current index).
3) If the stack is not empty, then one by one remove all bars from stack and do step 2.b for every removed bar.
Following is implementation of the above algorithm.
# title : 'LargestRectangularAreainaHistogram2.py'
# This function calculates maximum rectangular area under given histogram with n bars
def max_area_histogram(histogram):
# Create an empty stack. The stack holds indexes of histogram[] list.
# The bars stored in the stack are always in increasing order of their heights.
stack = list()
max_area = 0 # Initialize max area
# Run through all bars of given histogram
index = 0
while index < len(histogram):
# If this bar is higher than the bar on top stack, push it to stack
if (not stack) or (histogram[stack[-1]] <= histogram[index]):
stack.append(index)
index += 1
# If this bar is lower than top of stack, then calculate area of rectangle with
# stack top as the smallest (or minimum height) bar.'i' is 'right index' for
# the top and element before top in stack is 'left index'
else:
# pop the top
top_of_stack = stack.pop()
# Calculate the area with histogram[top_of_stack] stack as smallest bar
area = (histogram[top_of_stack] * ((index - stack[-1] - 1) if stack else index))
# update max area, if needed
max_area = max(max_area, area)
# Now pop the remaining bars from stack and calculate area with every popped bar as the smallest bar
while stack:
# pop the top
top_of_stack = stack.pop()
# Calculate the area with histogram[top_of_stack] stack as smallest bar
area = (histogram[top_of_stack] * ((index - stack[-1] - 1) if stack else index))
# update max area, if needed
max_area = max(max_area, area)
# Return maximum area under the given histogram
return max_area
# Driver Code
hist = [6, 2, 5, 4, 5, 1, 6]
print("Maximum area is", max_area_histogram(hist))
# Output
# Maximum area is 12
Time Complexity: Since every bar is pushed and popped only once, the time complexity of this method is \(\underline{O(n)}\).
2.2 Solution 2
By finding next smaller element and previous smaller element for every element in \(O(n)\) time complexity and \(O(n)\) auxiliary space .
Step 1 : First we will take two arrays left_smaller[] and right_smaller[] and initialize it with -1 and n respectively.
Step 2 : For every element we will store the index of previous smaller and next smaller element in left_smaller[] and right_smaller[] arrays respectively. It will take \(O(n)\) time.
Step 3 : Now for every element we will calculate area by taking this ith element as the smallest in the range left_smaller[i] and right_smaller[i] and multiplying it with the difference of left_smaller[i] and right_smaller[i].
Step 4 : We can find the maximum of all the area calculated in step 3 to get the desired maximum area.
def getMaxArea(arr):
s = [-1]
n = len(arr)
area = 0
i = 0
left_smaller = [-1]*n
right_smaller = [n]*n
while i < n:
while s and (s[-1] != -1) and (arr[s[-1]] > arr[i]):
right_smaller[s[-1]] = i
s.pop()
if((i > 0) and (arr[i] == arr[i-1])):
left_smaller[i] = left_smaller[i-1]
else:
left_smaller[i] = s[-1]
s.append(i)
i += 1
for j in range(0, n):
area = max(area, arr[j]*(right_smaller[j]-left_smaller[j]-1))
return area
hist = [6, 2, 5, 4, 5, 1, 6]
print("maxArea = ", getMaxArea(hist))