Range Query
The Port of Rotterdam, 1907, Paul Signac
We have an array arr[0 . . . n-1]. We should be able to efficiently find the value(min,max or sum etc) from index qs (query start) to qe (query end) where 0 <= qs <= qe <= n-1.
There are many ways.
1. Segment Tree
1.1 What is Segment Tree?
A segment tree is a data structure with the following characteristics.
- Leaf Nodes are the elements of the input array.
- Each internal node represents some merging(min,max or sum etc) of the leaf nodes. For this problem, merging is sum of leaves under a node.
- An array representation of tree is used to represent Segment Trees. For each node at index
i, the left child is at index2*i+1, right child at2*i+2and the parent is at(i – 1) / 2.
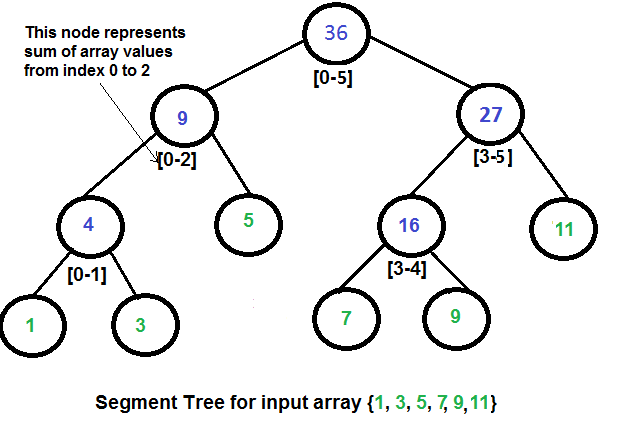
Segment tree look in memory
Like Heap, the segment tree is also represented as an array.
The difference here is, it is not a complete binary tree. It is rather a full binary tree (every node has 0 or 2 children) and all levels are filled except possibly the last level. Unlike Heap, the last level may have gaps between nodes. Below are the values in the segment tree array for the above diagram.
Below is memory representation of segment tree for input array {1, 3, 5, 7, 9, 11}
st[] = {36, 9, 27, 4, 5, 16, 11, 1, 3, DUMMY, DUMMY, 7, 9, DUMMY, DUMMY}
The dummy values are never accessed and have no use. This is some wastage of space due to simple array representation. We may optimize this wastage using some clever implementations, but code for sum and update becomes more complex.
1.2 Operations of Segment Tree
Construction from given array
- Start with a segment
arr[0 . . . n-1]. - Every time divide the current segment into two halves(if it has not yet become a segment of length 1), and then call the same procedure on both halves, and for each such segment, store the value(min, max or sum) in the corresponding node.
- All levels of the constructed segment tree will be completely filled except the last level. Also, the tree will be a Full Binary Tree because we always divide segments in two halves at every level. Since the constructed tree is always a full binary tree with n leaves, there will be
n-1internal nodes. So the total number of nodes will be2*n – 1. Note that this does not include dummy nodes.
Total size of the array representing segment tree
If n is a power of 2
- There are no dummy nodes. So the size of the segment tree is 2n-1 (n leaf nodes and n-1 internal nodes).
If n is not a power of 2
- The size of the tree will be 2*x – 1 where x is the smallest power of 2 greater than n.
- For example, when n = 10, then size of array representing segment tree is 2*16-1 = 31.
An alternate explanation for size is based on heignt. Height of the segment tree will be \(log_2n\). Since the tree is represented using array and relation between parent and child indexes must be maintained, size of memory allocated for segment tree will be \(\underline{2 * 2^{log_2n} – 1}\).
Query for Sum
Once the tree is constructed, how to get the sum using the constructed segment tree.
/* Algorithm to get the sum of elements */
int getSum(node, l, r)
{
if the range of the node is within l and r
return value in the node
else if the range of the node is completely outside l and r
return 0
else
return getSum(node's left child, l, r) + getSum(node's right child, l, r)
}
Update a value
Like tree construction and query operations, the update can also be done recursively. Let diff be the value to be added. We start from the root of the segment tree and add diff to all nodes which have given index in their range. If a node doesn’t have a given index in its range, don’t make any changes to that node.
1.3 Range Sum Query
1.3.1 Implementation using Segment Tree
# title : 'RangeSumQuerySegmentTree.py'
# Segment Tree operations(construction, query and update)
from math import ceil, log2;
# A utility function to get the middle index from corner indexes.
def getMid(s, e) :
return s + (e -s) // 2;
""" A recursive function to get the sum of values in the given range of the array.
The following are parameters for this function.
st --> Pointer to segment tree
si --> Index of current node in the segment tree. Initially 0 is passed as root is always at index 0
ss & se --> Starting and ending indexes of the segment represented by current node, i.e., st[si]
qs & qe --> Starting and ending indexes of query range """
def getSumUtil(st, ss, se, qs, qe, si) :
# If segment of this node is a part of given range, then return the sum of the segment
if (qs <= ss and qe >= se) :
return st[si];
# If segment of this node is outside the given range
if (se < qs or ss > qe) :
return 0;
# If a part of this segment overlaps with the given range
mid = getMid(ss, se);
return getSumUtil(st, ss, mid, qs, qe, 2 * si + 1) +
getSumUtil(st, mid + 1, se, qs, qe, 2 * si + 2);
""" A recursive function to update the nodes which have the given index in their range.
The following are parameters st, si, ss and se are same as getSumUtil()
i --> index of the element to be updated. This index is in the input array.
diff --> Value to be added to all nodes which have i in range """
def updateValueUtil(st, ss, se, i, diff, si) :
# Base Case: If the input index lies outside the range of this segment
if (i < ss or i > se) :
return;
# If the input index is in range of this node, then update the value of the node and its children
st[si] = st[si] + diff;
if (se != ss) :
mid = getMid(ss, se);
updateValueUtil(st, ss, mid, i, diff, 2 * si + 1);
updateValueUtil(st, mid + 1, se, i, diff, 2 * si + 2);
# The function to update a value in input array and segment tree
# It uses updateValueUtil() to update the value in segment tree
def updateValue(arr, st, n, i, new_val) :
# Check for erroneous input index
if (i < 0 or i > n - 1) :
print("Invalid Input", end = "");
return;
# Get the difference between new value and old value
diff = new_val - arr[i];
# Update the value in array
arr[i] = new_val;
# Update the values of nodes in segment tree
updateValueUtil(st, 0, n - 1, i, diff, 0);
# Return sum of elements in range from index qs (query start) to qe (query end)
# It mainly uses getSumUtil()
def getSum(st, n, qs, qe) :
# Check for erroneous input values
if (qs < 0 or qe > n - 1 or qs > qe) :
print("Invalid Input", end = "");
return -1;
return getSumUtil(st, 0, n - 1, qs, qe, 0);
# A recursive function that constructs Segment Tree for array[ss..se].
# si is index of current node in segment tree st
def constructSTUtil(arr, ss, se, st, si) :
# If there is one element in array, store it in current node of segment tree and return
if (ss == se) :
st[si] = arr[ss];
return arr[ss];
# If there are more than one elements, then recur for left and right subtrees and store the sum of values in this node
mid = getMid(ss, se);
st[si] = constructSTUtil(arr, ss, mid, st, si * 2 + 1) + constructSTUtil(arr, mid + 1, se, st, si * 2 + 2);
return st[si];
""" Function to construct segment tree from given array.
This function allocates memory for segment tree and
calls constructSTUtil() to fill the allocated memory """
def constructST(arr, n) :
# Allocate memory for the segment tree
# Height of segment tree
x = (int)(ceil(log2(n)));
# Maximum size of segment tree
max_size = 2 * (int)(2**x) - 1;
# Allocate memory
st = [0] * max_size;
# Fill the allocated memory st
constructSTUtil(arr, 0, n - 1, st, 0);
# Return the constructed segment tree
return st;
# Driver Code
if __name__ == "__main__" :
arr = [1, 3, 5, 7, 9, 11];
n = len(arr);
# Build segment tree from given array
st = constructST(arr, n);
# Print sum of values in array from index 1 to 3
print("Sum of values in given range = ",
getSum(st, n, 1, 3));
# Update: set arr[1] = 10 and update corresponding segment tree nodes
updateValue(arr, st, n, 1, 10);
# Find sum after the value is updated
print("Updated sum of values in given range = ", getSum(st, n, 1, 3), end = "");
1.3.2 Efficient implementation
Let us consider the following problem to understand Segment Trees without recursion. We have an array arr[0 . . . n-1]. We should be able to,
Find the sum of elements from index l to r where 0 <= l <= r <= n-1 Change the value of a specified element of the array to a new value x. We need to do arr[i] = x where 0 <= i <= n-1.
A simple solution is to run a loop from l to r and calculate the sum of elements in the given range. To update a value, simply do arr[i] = x. The first operation takes O(n) time and the second operation takes O(1) time.
Another solution is to create another array and store the sum from start to i at the ith index in this array. The sum of a given range can now be calculated in O(1) time, but the update operation takes O(n) time now. This works well if the number of query operations is large and there are very few updates.
What if the number of queries and updates are equal? Can we perform both the operations in O(log n) time once given the array? We can use a Segment Tree to do both operations in O(logn) time. We have discussed the complete implementation of segment trees in our previous post. In this post, we will discuss the easier and yet efficient implementation of segment trees than in the previous post.
Consider the array and segment tree as shown below:

You can see from the above image that the original array is at the bottom and is 0-indexed with 16 elements. The tree contains a total of 31 nodes where the leaf nodes or the elements of the original array start from node 16. So, we can easily construct a segment tree for this array using a 2N sized array where N is the number of elements in the original array. The leaf nodes will start from index N in this array and will go up to index (2N – 1). Therefore, the element at index i in the original array will be at index (i + N) in the segment tree array. Now to calculate the parents, we will start from the index (N – 1) and move upward. For index i , the left child will be at (2 * i) and the right child will be at (2i + 1) index. So the values at nodes at (2 * i) and (2i + 1) are combined at i-th node to construct the tree.
As you can see in the above figure, we can query in this tree in an interval [L,R) with left index(L) included and right (R) excluded.
We will implement all of these multiplication and addition operations using bitwise operators.
# title:'efficientSegmentTree.py'
# limit for array size
N = 100000;
# Max size of tree
tree = [0] * (2 * N);
# function to build the tree
def build(arr) :
# insert leaf nodes in tree
for i in range(n) :
tree[n + i] = arr[i];
# build the tree by calculating parents
for i in range(n - 1, 0, -1) :
tree[i] = tree[i << 1] + tree[i << 1 | 1];
# function to update a tree node
def updateTreeNode(p, value) :
# set value at position p
tree[p + n] = value;
p = p + n;
# move upward and update parents
i = p;
while i > 1 :
tree[i >> 1] = tree[i] + tree[i ^ 1];
i >>= 1;
# function to get sum on interval [l, r)
def query(l, r) :
res = 0;
# loop to find the sum in the range
l += n;
r += n;
while l < r :
if (l & 1) :
res += tree[l];
l += 1
if (r & 1) :
r -= 1;
res += tree[r];
l >>= 1;
r >>= 1
return res;
# Driver Code
if __name__ == "__main__" :
a = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12];
# n is global
n = len(a);
# build tree
build(a);
# print the sum in range(1,2) index-based
print(query(1, 3));
# modify element at 2nd index
updateTreeNode(2, 1);
# print the sum in range(1,2) index-based
print(query(1, 3));
# Output:
# 5
# 3
The complete implementation of the segment tree includes the query and update functions in a lower number of lines of code than the previous recursive one. Let us now understand how each of the functions works:
- The picture makes it clear that the leaf nodes are stored at i+n, so we can clearly insert all leaf nodes directly.
- The next step is to build the tree and it takes O(n) time. The parent always has its less index than its children, so we just process all the nodes in decreasing order, calculating the value of the parent node. If the code inside the build function to calculate parents seems confusing, then you can see this code. It is equivalent to that inside the build function.
tree[i]=tree[2*i]+tree[2*i+1] Updating a value at any position is also simple and the time taken will be proportional to the height of the tree. We only update values in the parents of the given node which is being changed. So to get the parent, we just go up to the parent node, which is p/2 or p»1, for node p. p^1 turns (2i) to (2i + 1) and vice versa to get the second child of p.
- Computing the sum also works in O(log(n)) time. If we work through an interval of [3,11), we need to calculate only for nodes 19,26,12, and 5 in that order.
The idea behind the query function is whether we should include an element in the sum or whether we should include its parent. Let’s look at the image once again for proper understanding. Consider that L is the left border of an interval and R is the right border of the interval [L,R). It is clear from the image that if L is odd, then it means that it is the right child of its parent and our interval includes only L and not the parent. So we will simply include this node to sum and move to the parent of its next node by doing L = (L+1)/2. Now, if L is even, then it is the left child of its parent and the interval includes its parent also unless the right borders interfere. Similar conditions are applied to the right border also for faster computation. We will stop this iteration once the left and right borders meet.
The theoretical time complexities of both previous implementation and this implementation is the same, but practically, it is found to be much more efficient as there are no recursive calls. We simply iterate over the elements that we need. Also, this is very easy to implement.
1.3 Range Minumum Query
A simple solution is to run a loop from qs to qe and find minimum element in given range. This solution takes O(n) time in worst case.
Another solution is to create a 2D array where an entry [i, j] stores the minimum value in range arr[i..j]. Minimum of a given range can now be calculated in O(1) time, but preprocessing takes O(n^2) time. Also, this approach needs O(n^2) extra space which may become huge for large input arrays.
Segment tree can be used to do preprocessing and query in moderate time. With a segment tree, preprocessing time is O(n) and the time complexity for a range minimum query is O(logn). The extra space required is O(n) to store the segment tree.
Representation of Segment trees
- Leaf Nodes are the elements of the input array.
- Each internal node represents minimum of all leaves under it. An array representation of tree is used to represent Segment Trees. For each node at index i, the left child is at index
2*i+1, right child at2*i+2and the parent is at(i – 1) / 2.
Construction of Segment Tree
We start with a segment arr[0 . . . n-1]. and every time we divide the current segment into two halves(if it has not yet become a segment of length 1), and then call the same procedure on both halves, and for each such segment, we store the minimum value in a segment tree node. All levels of the constructed segment tree will be completely filled except the last level. Also, the tree will be a Full Binary Tree because we always divide segments in two halves at every level. Since the constructed tree is always full binary tree with n leaves, there will be n-1 internal nodes. So total number of nodes will be 2*n – 1. Height of the segment tree will be ⌈log₂n⌉. Since the tree is represented using array and relation between parent and child indexes must be maintained, size of memory allocated for segment tree will be 2 * 2⌈log2n⌉ – 1.
Query for minimum value Once the tree is constructed, how to do range minimum query using the constructed segment tree. Following is algorithm to get the minimum.
// qs --> query start index, qe --> query end index
int RMQ(node, qs, qe)
{
if range of node is within qs and qe
return value in node
else if range of node is completely outside qs and qe
return INFINITE
else
return min( RMQ(node's left child, qs, qe), RMQ(node's right child, qs, qe) )
}
# title : 'RangeMinumumQuerySegmentTree.py'
import sys;
from math import ceil,log2;
INT_MAX = sys.maxsize;
# A utility function to get minimum of two numbers
def minVal(x, y) :
return x if (x < y) else y;
# A utility function to get the middle index from corner indexes.
def getMid(s, e) :
return s + (e - s) // 2;
""" A recursive function to get the minimum value in a given range of array indexes.
The following are parameters for this function.
st --> Pointer to segment tree
index --> Index of current node in the segment tree. Initially 0 is passed as root is always at index 0
ss & se --> Starting and ending indexes of the segment represented by current node, i.e., st[index]
qs & qe --> Starting and ending indexes of query range """
def RMQUtil( st, ss, se, qs, qe, index) :
# If segment of this node is a part of given range, then return the min of the segment
if (qs <= ss and qe >= se) :
return st[index];
# If segment of this node is outside the given range
if (se < qs or ss > qe) :
return INT_MAX;
# If a part of this segment overlaps with the given range
mid = getMid(ss, se);
return minVal(RMQUtil(st, ss, mid, qs, qe, 2 * index + 1), RMQUtil(st, mid + 1, se, qs, qe, 2 * index + 2));
# Return minimum of elements in range from index qs (query start) to qe (query end). It mainly uses RMQUtil()
def RMQ( st, n, qs, qe) :
# Check for erroneous input values
if (qs < 0 or qe > n - 1 or qs > qe) :
print("Invalid Input");
return -1;
return RMQUtil(st, 0, n - 1, qs, qe, 0);
# A recursive function that constructs Segment Tree for array[ss..se].
# si is index of current node in segment tree st
def constructSTUtil(arr, ss, se, st, si) :
# If there is one element in array, store it in current node of segment tree and return
if (ss == se) :
st[si] = arr[ss];
return arr[ss];
# If there are more than one elements, then recur for left and right subtrees
# and store the minimum of two values in this node
mid = getMid(ss, se);
st[si] = minVal(constructSTUtil(arr, ss, mid, st, si * 2 + 1), constructSTUtil(arr, mid + 1, se, st, si * 2 + 2));
return st[si];
"""Function to construct segment tree from given array. This function allocates
memory for segment tree and calls constructSTUtil() to fill the allocated memory """
def constructST( arr, n) :
# Allocate memory for segment tree
# Height of segment tree
x = (int)(ceil(log2(n)));
# Maximum size of segment tree
max_size = 2 * (int)(2**x) - 1;
st = [0] * (max_size);
# Fill the allocated memory st
constructSTUtil(arr, 0, n - 1, st, 0);
# Return the constructed segment tree
return st;
# Driver Code
if __name__ == "__main__" :
arr = [1, 3, 2, 7, 9, 11];
n = len(arr);
# Build segment tree from given array
st = constructST(arr, n);
qs = 1; # Starting index of query range
qe = 5; # Ending index of query range
# Print minimum value in arr[qs..qe]
print("Minimum of values in range [", qs,
",", qe, "]", "is =", RMQ(st, n, qs, qe));
1.5 Lazy Propagation
What if there are updates on a range of array indexes?
For example add 10 to all values at indexes from 2 to 7 in array. The above update has to be called for every index from 2 to 7. We can avoid multiple calls by writing a function updateRange() that updates nodes accordingly.
Lazy Propagation – An optimization to make range updates faster
When there are many updates and updates are done on a range, we can postpone some updates (avoid recursive calls in update) and do those updates only when required.
Please remember that a node in segment tree stores or represents result of a query for a range of indexes. And if this node’s range lies within the update operation range, then all descendants of the node must also be updated. For example consider the node with value 27 in above diagram, this node stores sum of values at indexes from 3 to 5. If our update query is for range 2 to 5, then we need to update this node and all descendants of this node. With Lazy propagation, we update only node with value 27 and postpone updates to its children by storing this update information in separate nodes called lazy nodes or values. We create an array lazy[] which represents lazy node. Size of lazy[] is same as array that represents segment tree, which is tree[] in below code.
The idea is to initialize all elements of lazy[] as 0. A value 0 in lazy[i] indicates that there are no pending updates on node i in segment tree. A non-zero value of lazy[i] means that this amount needs to be added to node i in segment tree before making any query to the node.
Below is modified update method.
// To update segment tree for change in array
// values at array indexes from us to ue.
updateRange(us, ue)
1) If current segment tree node has any pending
update, then first add that pending update to
current node.
2) If current node's range lies completely in
update query range.
....a) Update current node
....b) Postpone updates to children by setting
lazy value for children nodes.
3) If current node's range overlaps with update
range, follow the same approach as above simple
update.
...a) Recur for left and right children.
...b) Update current node using results of left
and right calls.
Is there any change in Query Function also?
Since we have changed update to postpone its operations, there may be problems if a query is made to a node that is yet to be updated. So we need to update our query method also which is getSumUtil in previous post. The getSumUtil() now first checks if there is a pending update and if there is, then updates the node. Once it makes sure that pending update is done, it works same as the previous getSumUtil().
# title: 'LazyPropagtionInSegmentTree.py'
MAX = 1000
# Ideally, we should not use global variables and large constant-sized arrays,
# we have done it here for simplicity.
tree = [0] * MAX; # To store segment tree
lazy = [0] * MAX; # To store pending updates
""" si -> index of current node in segment tree
ss and se -> Starting and ending indexes of elements for which current nodes stores sum.
us and ue -> starting and ending indexes of update query
diff -> which we need to add in the range us to ue """
def updateRangeUtil(si, ss, se, us, ue, diff) :
# If lazy value is non-zero for current node of segment tree, then there are some pending updates.
# So we need to make sure that the pending updates are done before making new updates.
# Because this value may be used by parent after recursive calls (See last line of this function)
if (lazy[si] != 0) :
# Make pending updates using value stored in lazy nodes
tree[si] += (se - ss + 1) * lazy[si];
# checking if it is not leaf node because if it is leaf node then we cannot go further
if (ss != se) :
# We can postpone updating children we don't # need their new values now.
# Since we are not yet updating children of si, # we need to set lazy flags for the children
lazy[si * 2 + 1] += lazy[si];
lazy[si * 2 + 2] += lazy[si];
# Set the lazy value for current node # as 0 as it has been updated
lazy[si] = 0;
# out of range
if (ss > se or ss > ue or se < us) :
return ;
# Current segment is fully in range
if (ss >= us and se <= ue) :
# Add the difference to current node
tree[si] += (se - ss + 1) * diff;
# same logic for checking leaf node or not
if (ss != se) :
# This is where we store values in lazy nodes, rather than updating the segment tree itself
# Since we don't need these updated values now we postpone updates by storing values in lazy[]
lazy[si * 2 + 1] += diff;
lazy[si * 2 + 2] += diff;
return;
# If not completely in rang, but overlaps, recur for children,
mid = (ss + se) // 2;
updateRangeUtil(si * 2 + 1, ss, mid, us, ue, diff);
updateRangeUtil(si * 2 + 2, mid + 1, se, us, ue, diff);
# And use the result of children calls to update this node
tree[si] = tree[si * 2 + 1] + tree[si * 2 + 2];
# Function to update a range of values in segment tree
''' us and eu -> starting and ending indexes of update query
ue -> ending index of update query
diff -> which we need to add in the range us to ue '''
def updateRange(n, us, ue, diff) :
updateRangeUtil(0, 0, n - 1, us, ue, diff);
''' A recursive function to get the sum of values in given range of the array.
The following are parameters for this function.
si --> Index of current node in the segment tree. Initially 0 is passed as root is always at'index 0
ss & se --> Starting and ending indexes of the segment represented by current node, i.e., tree[si]
qs & qe --> Starting and ending indexes of query range '''
def getSumUtil(ss, se, qs, qe, si) :
# If lazy flag is set for current node of segment tree, then there are some pending updates.
# So we need to make sure that the pending updates are done before processing the sub sum query
if (lazy[si] != 0) :
# Make pending updates to this node. Note that this node represents sum of
# elements in arr[ss..se] and all these elements must be increased by lazy[si]
tree[si] += (se - ss + 1) * lazy[si];
# checking if it is not leaf node because if it is leaf node then we cannot go further
if (ss != se) :
# Since we are not yet updating children os si, we need to set lazy values for the children
lazy[si * 2 + 1] += lazy[si];
lazy[si * 2 + 2] += lazy[si];
# unset the lazy value for current node as it has been updated
lazy[si] = 0;
# Out of range
if (ss > se or ss > qe or se < qs) :
return 0;
# At this point we are sure that pending lazy updates are done for current node.
# So we can return value (same as it was for query in our previous post)
# If this segment lies in range
if (ss >= qs and se <= qe) :
return tree[si];
# If a part of this segment overlaps with the given range
mid = (ss + se) // 2;
return (getSumUtil(ss, mid, qs, qe, 2 * si + 1) +
getSumUtil(mid + 1, se, qs, qe, 2 * si + 2));
# Return sum of elements in range from index qs (query start) to qe (query end).
# It mainly uses getSumUtil()
def getSum(n, qs, qe) :
# Check for erroneous input values
if (qs < 0 or qe > n - 1 or qs > qe) :
print("Invalid Input");
return -1;
return getSumUtil(0, n - 1, qs, qe, 0);
# A recursive function that constructs Segment Tree for array[ss..se].
# si is index of current node in segment tree st.
def constructSTUtil(arr, ss, se, si) :
# out of range as ss can never be greater than se
if (ss > se) :
return ;
# If there is one element in array, store it in current node of segment tree and return
if (ss == se) :
tree[si] = arr[ss];
return;
# If there are more than one elements, then recur for left and right subtrees and store the sum of values in this node
mid = (ss + se) // 2;
constructSTUtil(arr, ss, mid, si * 2 + 1);
constructSTUtil(arr, mid + 1, se, si * 2 + 2);
tree[si] = tree[si * 2 + 1] + tree[si * 2 + 2];
''' Function to construct segment tree from given array. This function allocates memory
for segment tree and calls constructSTUtil() to fill the allocated memory '''
def constructST(arr, n) :
# Fill the allocated memory st
constructSTUtil(arr, 0, n - 1, 0);
# Driver Code
if __name__ == "__main__" :
arr = [1, 3, 5, 7, 9, 11];
n = len(arr);
# Build segment tree from given array
constructST(arr, n);
# Print sum of values in array from index 1 to 3
print("Sum of values in given range =", getSum(n, 1, 3));
# Add 10 to all nodes at indexes from 1 to 5.
updateRange(n, 1, 5, 10);
# Find sum after the value is updated
print("Updated sum of values in given range =", getSum( n, 1, 3));
# Output:
# Sum of values in given range = 15
# Updated sum of values in given range = 45
1.6 Time Complexities
Tree Construction : \(O(n)\)
Query in Range : \(O(logn)\)
Updating an element : \(O(logn)\).
2. Sparse Table
COMING SOON,,,