Recursive Function
Comblat-le-Château, the Meadow Le Pré, Opus 161, 1887, Paul Signac
- 1. What is Recursive Function?
- 2. Exit condition for Recursive Function
- 3. Factorial Implementation
- 4. Computing the greatest common divisor (Euclidean Algorithm)
1. What is Recursive Function?
A recursive function is a function that calls itself directly or indirectly.
A simple example of a recursive function
- Infinitely prints the string ‘Call recursive function.’
- After outputting to a certain extent, a message exceeding the maximum recursion depth is output.
# Python
def recursive_function():
print('Call the recursive function.')
recursive_function()
recursive_function()
# A loop can be created without using a while or for statement.
When a function is called recursively, the function is repeatedly stacked on the computer system stack frame. That is, after the last function called is processed, the function that called the function is executed.
2. Exit condition for Recursive Function
In problem solving, the exit condition(base case) of the recursive function must be specified.
If the exit condition is not properly specified, it is called indefinitely.
Example of a recursive function with an exit condition.
# Python
def recursive_function(i):
# Specify an exit condition to terminate when the 100th call is made
if i == 100:
return
print(i, 'In the th recursive function', i+1, 'The th recursive function is called.')
recursive_function( i+1 ) # Automatically increment by 1 expression.
print(i, 'End the th recursive function.')
recursive_function(1)
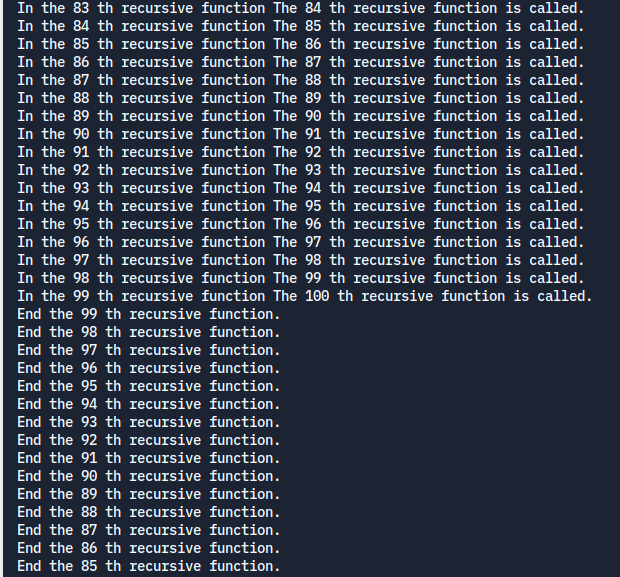
It is displayed that the 99th to the 1st are finished sequentially. If you use a recursive function, it comes out similar to putting data on the stack and then removing it.
3. Factorial Implementation
- n! = 1 x 2 x 3 x … x (n-1) x n
- Mathematically 0! = 1! = 1
Iteratively implementation of n!
# title:'FactorialIterative.py'
def factorial_iterative(n):
result = 1
# Multiply the numbers from 1 to n sequentially
for i in range(1, n+1):
result *= i
return result
Recursively implementation of n!
# title:'FactorialRecursive.py'
def factorial_recursive(n):
if n <= 1: # Returns 1 if n is 1 or less
return 1
#n! = n * (n-1)! as code
return n * factorial_recursive(n-1)
#n implemented in each way n! output(n=5)
print('Implemented iteratively: ', factorial_iterative(5))
print('Implemented recursively: ', factorial_recursive(5))
# Output
# Implemented iteratively: 120
# Implemented recursively: 120
Implementing it recursively makes the code more concise and intuitive.
4. Computing the greatest common divisor (Euclidean Algorithm)
Euclidean Algorithm
- For two natural numbers A and B (A > B), the remainder of dividing A by B is called R.
- In this case, the greatest common divisor of A and B is the same as the greatest common divisor of B and R.
The idea of Euclidean Algorithm can be written as a recursive function.
Example: GCD(192, 162)
| Step | A | B |
|---|---|---|
| 1 | 192 | 162 |
| 2 | 162 | 30 |
| 3 | 30 | 12 |
| 4 | 12 | 6 |
The form of changing the expression is repetitive and has the same structure. So, it can be made intuitively with a recursive function.
# title:'GCD.py'
def gcd(a, b):
if a % b == 0:
return b
else:
return gcd(b, a % b)
print(gcd(192, 162))
# Output
# 6
All recursive functions can implement the same function by using a loop.
In some cases, recursive functions are more advantageous than loops, and in other cases, they are disadvantageous.
When a computer calls a function successively, it is stacked on a stack frame inside the computer’s memory.
So, When we need to use the stack, recursive functions are often used instead of the stack library for implementation purposes. ex. DFS is sometimes implemented as a recursive function.
https://www.programiz.com/
https://www.geeksforgeeks.org/
https://blog.naver.com/PostList.naver?blogId=ndb796
이것이 코딩테스트다,2020,나동빈,한빛미디어