Tree

Antibes in the Morning, 1888, Claude Monet
1. Tree
1.1 What is Tree?
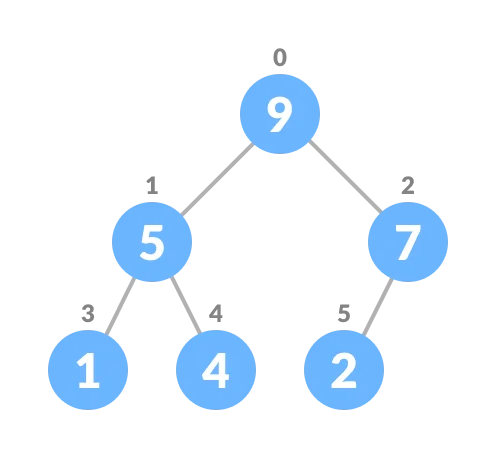
A tree data structure is a way to hold data that when visualized looks like a tree.
This is actually what we visualized a tree data structure to look like all data points in the tree are called nodes.
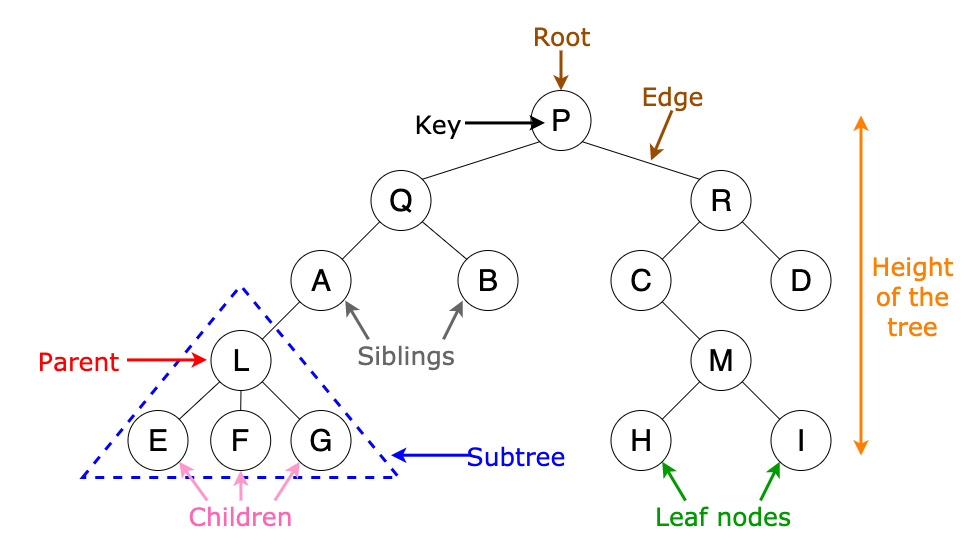
1.2 Tree Implementation
// title: 'Tree.js'
class Tree{
// The object created by the constructor becomes a Node in the tree.
constructor(value){
this.value = value;
this.children = [];
};
// It's important to remember what name the value is created with and where it is attached.
insertNode(value){
const childNode = new Tree(value);
this.children.push(childNode);
};
contains(value){
// Return true if it contains a value.
if(this.value === value){
return true
}
// Iterate through the childNodes, traversing the children array until a value is found.
for(i=0; i<this.collection.length; i++){
if(this.children[i].contains(value))
return true
}
// Return false if it's not found despite traversing all over.
return false
}
}
2. Binary Search Tree
2.1 What is Binary Search Tree?
Binary Tree’s each node can only has two branches.
Binary Search Trees are ordered. Each left subtree is less than or equal to the painter node. And each right subtree is greater than or equal to the parent node.
Because they use the principle of binary search. On average operations are able to skip about half of the tree so that each lookup insertion or deletion takes time proportional to the logarithm of the number of items stored in the tree.
This is much better than the linear time required to find items by key in an unsorted array but slower than the corresponding o perations on a hash table.
BST add operation

BST find operation
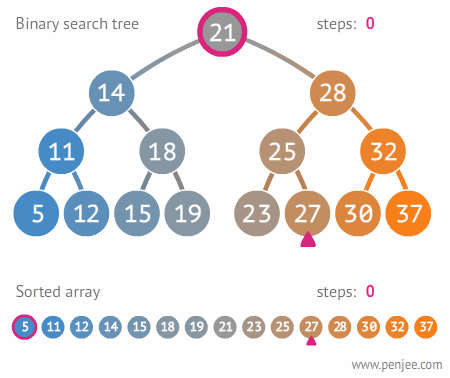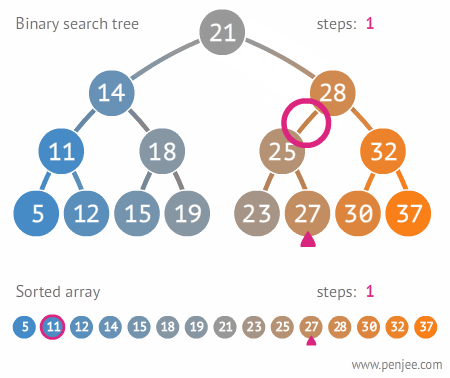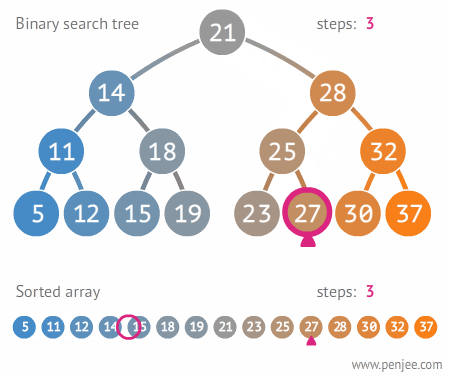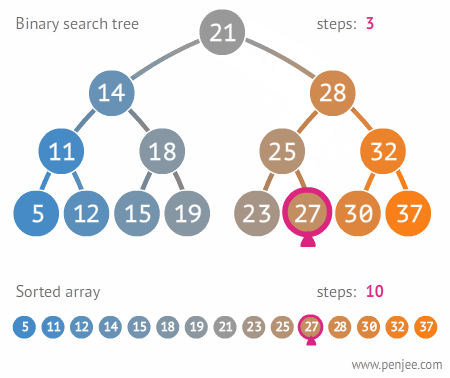
BST from ordered array
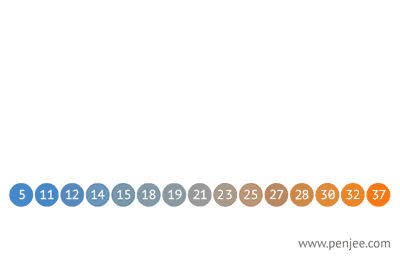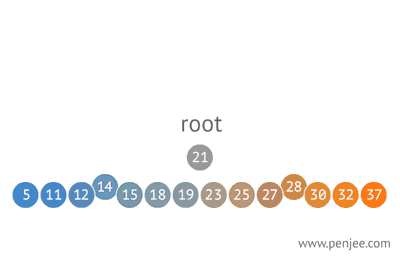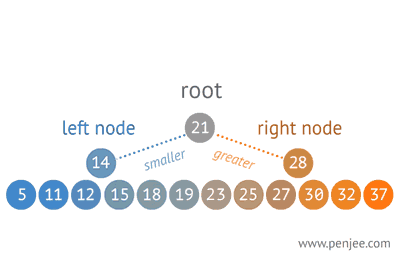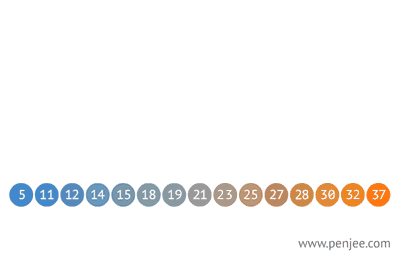
BST degeneration
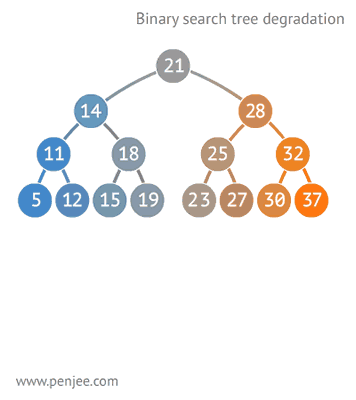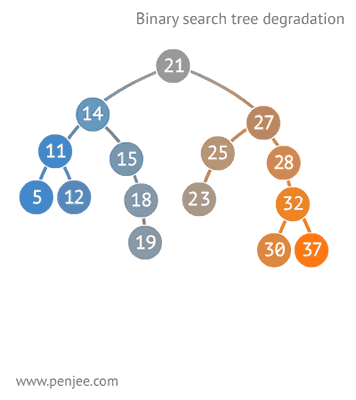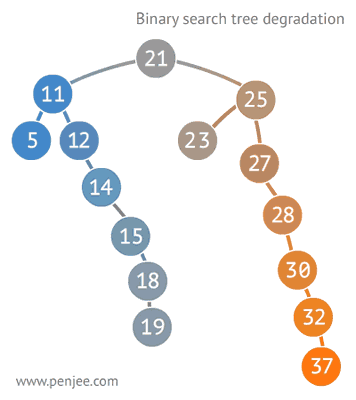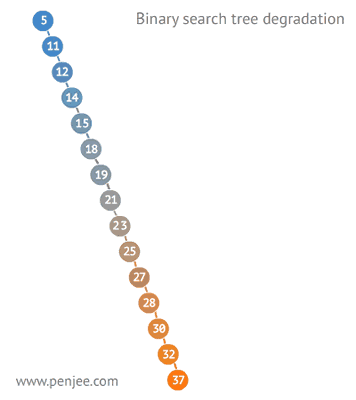
2.2 Binary Search Tree Traversal
BST inorder operation
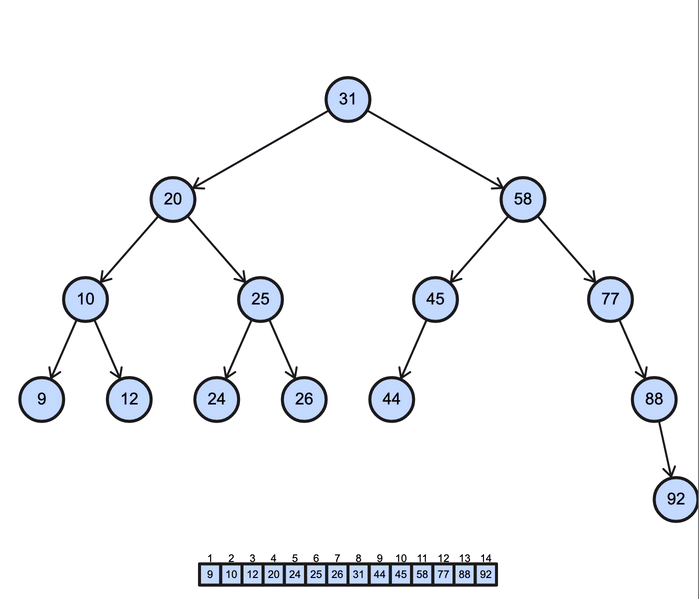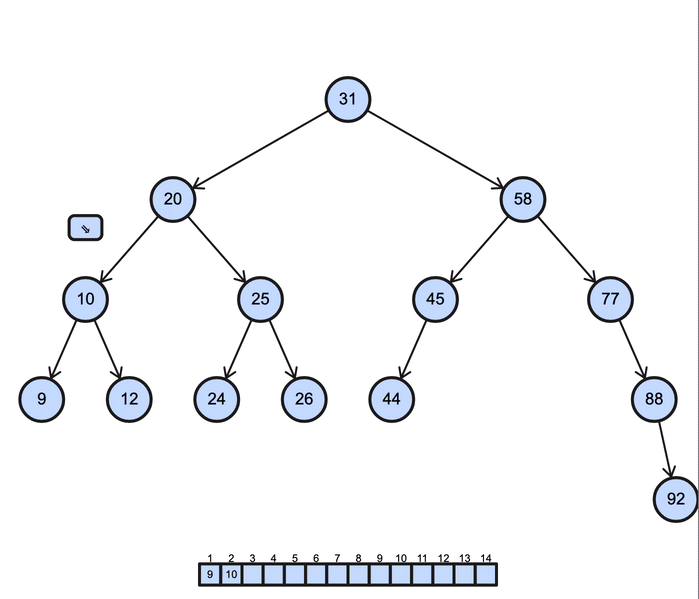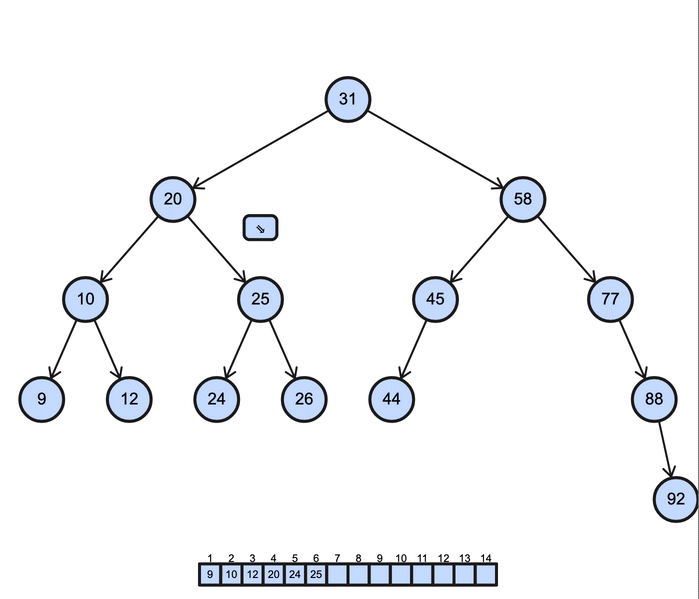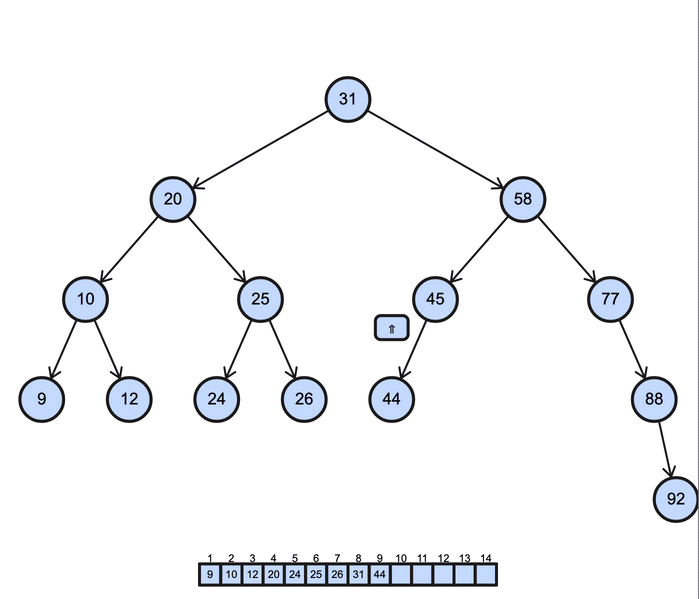
BST preorder operation (Depth-First Search)
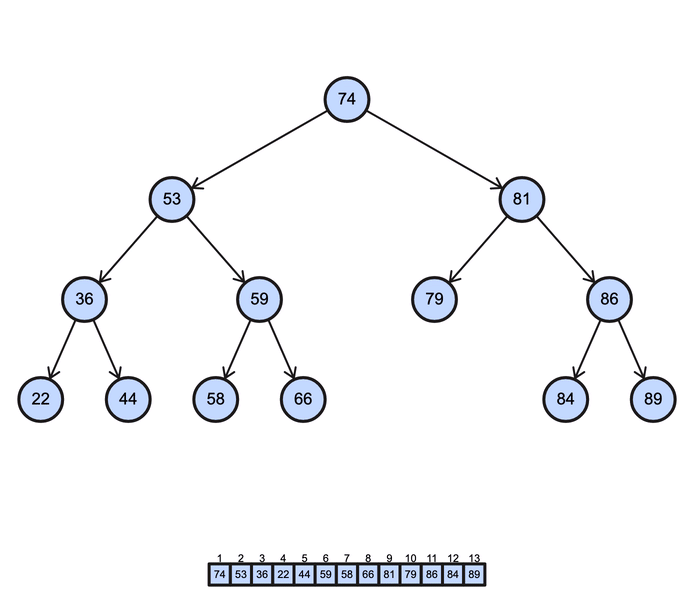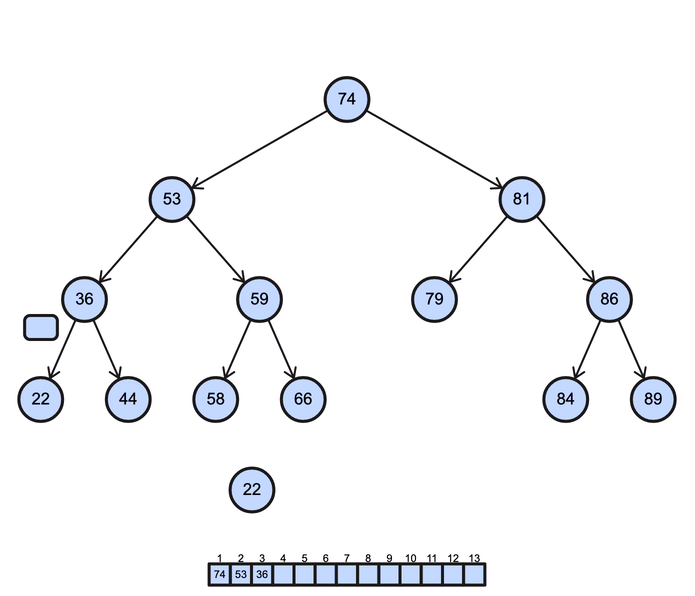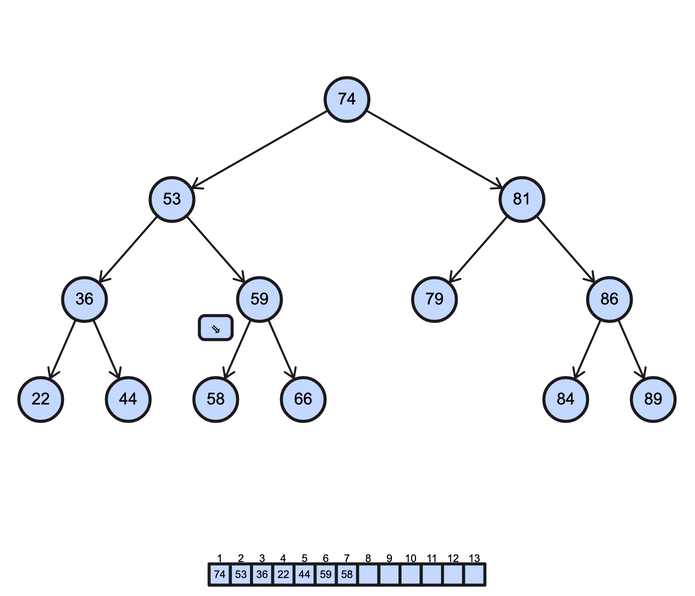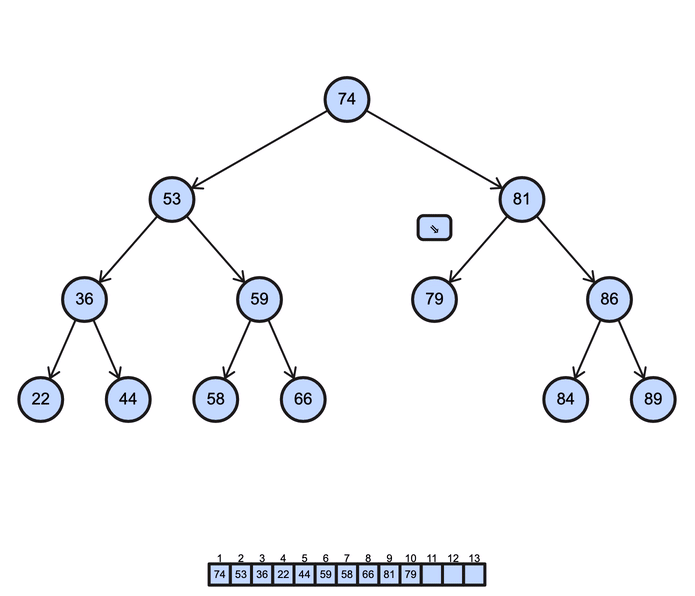
BST postorder operation
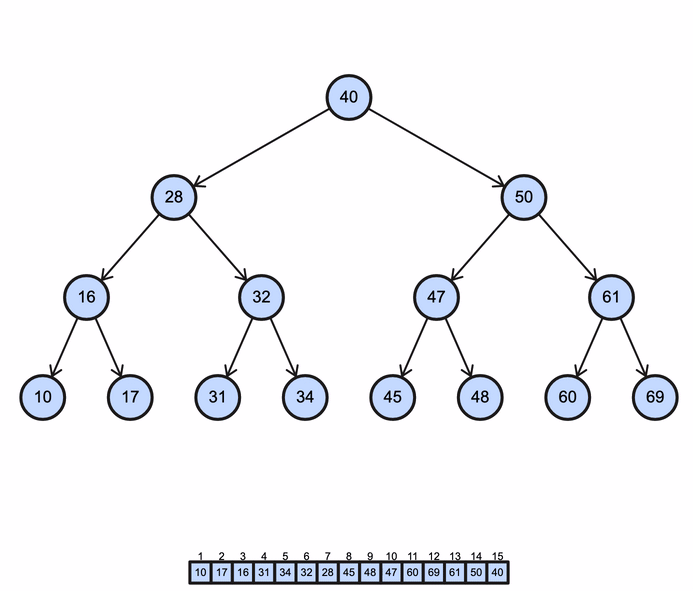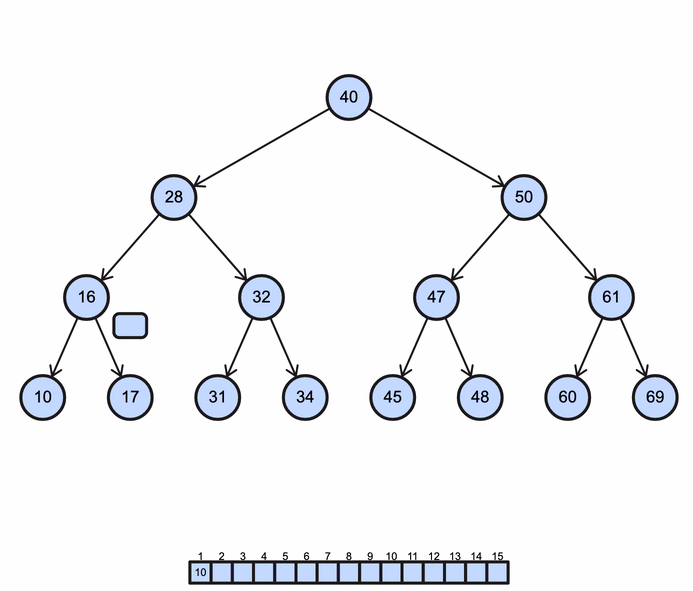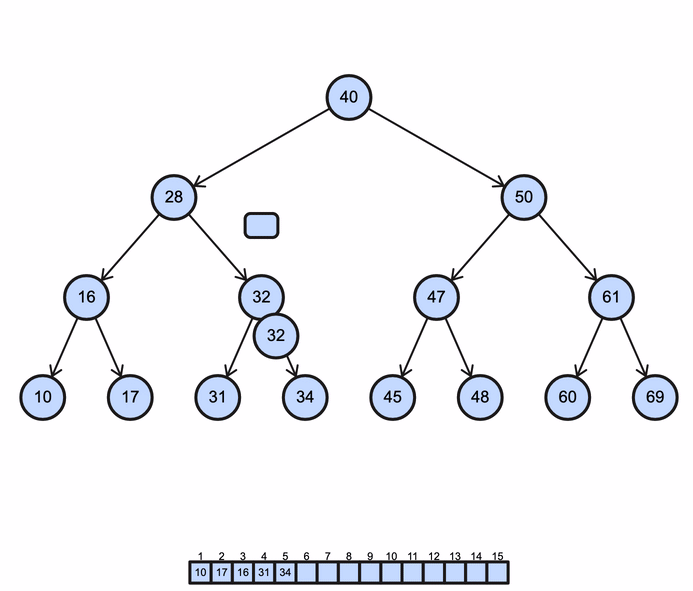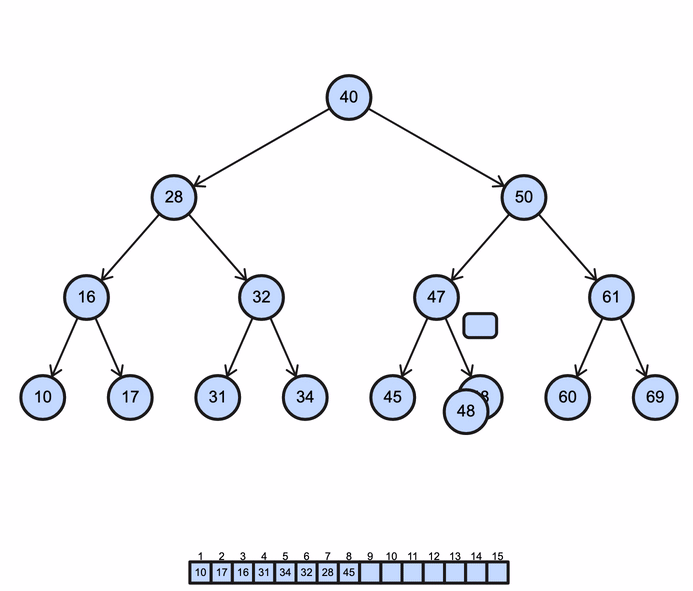
BST levelorder operation (Breadth-First Search)
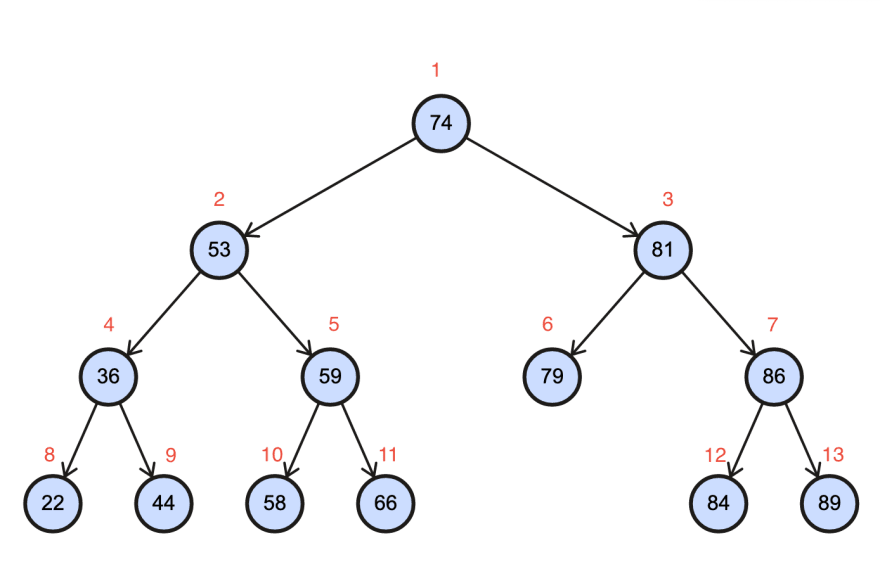
2.3 Binary Search Tree Implementation
// title: 'BinarySearchTree.js'
// The node class represents each node in the tree.
class Node {
constructor(data, left = null, right = null) {
this.data = data;
this.left = left;
this.right = right;
}
}
class BST {
//constructor which just creates the the root node which is the top of the tree.
constructor() {
this.root = null;
}
// This is how to add something to the tree.
add(data) {
const node = this.root; // Get a reference to the root node.
if(node === null) { // But if this is the first node, node will be null.
this.root = new Node(data); // Create node based on that data.
return;
} else {
const searchTree = function(node) { //Pass in the node which starts off as the root node.
if(data < node.data) { // If the data we pass in is less than node.data, put the node on the left side of the tree.
if(node.left === null) {
node.left = new Node(data);
return;
} else if (node.left !== null) {
return searchTree(node.left); // Continue working down the tree to find where to put the node.
}
} else if (data > node.data) { // If the data is more than no data, put the node on the right side.
if(node.right === null) {
node.right = new Node(data);
return;
} else if (node.right !== null) {
return searchTree(node.right); // Keep searching.
}
} else { // If they're equal, not going to add the data to the tree.
return null;
}
}
return searchTree(node);
}
}
// The minimum is all the way on the left side.
findMin() {
let current = this.root;
while (current.left !== null) {
current = current.left;
}
return current.data;
}
//The maximum is all the way on the right side.
findMax() {
let current = this.root;
while (current.right !== null) {
current = current.right;
}
return current.data;
}
find() {
let current = this.root;
while (current.data !== data) {
if (data < current.data) {
current = current.left;
} else {
current = current.right;
}
if (current === null) {
return null;
}
}
return current;
}
// isPresent is very similar to find but instead of returning the node, returning whether the data is in the tree (boolean).
isPresent(data) {
let current = this.root;
while (current) {
if (data === current.data) {
return true;
}
if (data < current.data) {
current = current.left;
} else {
current = current.right;
}
}
return false;
}
remove(data) {
const removeNode = function(node, data) {
if (node === null) { // First of all we have to check if we have an empty tree.
return null;
}
if (data === node.data) { // Found the node with the data.
if (node.left === null && node.right === null) { // node has no children.
return null; // Setting the reference to the node to null.
}
if (node.left === null) { // node has no left child.
return node.right;
}
if (node.left === null) { // node has no right child.
return node.right;
}
let tempNode = node.right; // node has two child.
// To remove and replace, first go to the right sub node and then go all the way down to the most left sub node.
while (tempNode.left !== null) {
tempNode = tempNode.left
}
node.data = tempNode.data;
node.right = removeNode(node.right, tempNode.data);
return node;
} else if (data < node.data) { // We have to go to the left side of the tree.
node.left = removeNode(node.left, data);
return node;
} else { // We have to go to the right side of the tree.
node.right = removeNode(node.right, data);
return node;
}
}
this.root = removeNode(this.root, data); // We're gonna pass in the root node, because you always start with the root node, and then the data that we're searching for.
}
isBalanced() {
return (this.findMinHeight() >= this.findMaxHeight() - 1)
}
findMinHeight(node = this.root) {
if (node == null) {
return -1;
};
let left = this.findMinHeight(node.left);
let right = this.findMinHeight(node.right);
if (left <br right) {
return left + 1;
} else {
return right + 1;
};
}
findMaxHeight(node = this.root) {
if (node == null) {
return -1;
};
let left = this.findMaxHeight(node.left);
let right = this.findMaxHeight(node.right);
if (left > right) {
return left + 1;
} else {
return right + 1;
};
}
inOrder() {
if (this.root == null) {
return null;
} else {
let result = new Array();
function traverseInOrder(node) {
node.left && traverseInOrder(node.left);
result.push(node.data);
node.right && traverseInOrder(node.right);
}
traverseInOrder(this.root);
return result;
};
}
preOrder() {
if (this.root == null) {
return null;
} else {
let result = new Array();
function traversePreOrder(node) {
result.push(node.data);
node.left && traversePreOrder(node.left);
node.right && traversePreOrder(node.right);
};
traversePreOrder(this.root);
return result;
};
}
postOrder() {
if (this.root == null) {
return null;
} else {
let result = new Array();
function traversePostOrder(node) {
node.left && traversePostOrder(node.left);
node.right && traversePostOrder(node.right);
result.push(node.data);
};
traversePostOrder(this.root);
return result;
}
}
levelOrder() {
let result = [];
let Q = [];
if (this.root != null) {
Q.push(this.root);
while(Q.length > 0) {
let node = Q.shift();
result.push(node.data);
if (node.left != null) {
Q.push(node.left);
};
if (node.right != null) {
Q.push(node.right);
};
};
return result;
} else {
return null;
};
};
}
const bst = new BST();
bst.add(4);
bst.add(2);
bst.add(6);
bst.add(3);
bst.add(5);
bst.add(7);
console.log(bst)
bst.remove(4);
console.log(bst.findMin()) // 2
console.log(bst.findMax()) // 7
bst.remove(7);
console.log(bst.findMax()) // 6
console.log(bst.isPresent(4)) // false
bst.add(9);
bst.add(1);
bst.add(22);
bst.add(20);
console.log(bst)
console.log(bst.findMinHeight()); // 1
console.log(bst.findMaxHeight()); // 4
console.log(bst.isBalanced()); // false
bst.add(10);
console.log(bst.findMinHeight()); // 1
console.log(bst.findMaxHeight()); // 5
console.log(bst.isBalanced()); // false
console.log('inOrder: ' + bst.inOrder()); // inOrder: 1,2,3,5,6,9,10,20,22
console.log('preOrder: ' + bst.preOrder()); // preOrder: 5,2,1,3,6,9,22,20,10
console.log('postOrder: ' + bst.postOrder()); // postOrder: 1,3,2,10,20,22,9,6,5
console.log('levelOrder: ' + bst.levelOrder()); // levelOrder: 5,2,6,1,3,9,22,20,10
3. Heap
3.1 What is Heap?
A complete binary tree is a binary tree in which all the levels are completely filled except possibly the lowest one, which is filled from the left.
Heap data structure is a complete binary tree that satisfies the heap property, where any given node is
always smaller than the child node/s and the key of the root node is the smallest among all other nodes. This property is also called min heap property.
always greater than its child node/s and the key of the root node is the largest among all other nodes. This property is also called max heap property.
The heap always removes the root note first.
Min Heap
- The root note has the smallest value.
- Therefore, the data with the smallest value is removed first.
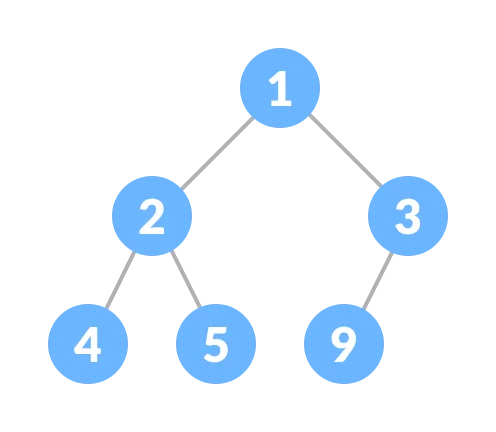
Min-Heap
Max Heap
- The root node has the largest value.
- Therefore, the data with the large value is removed first.
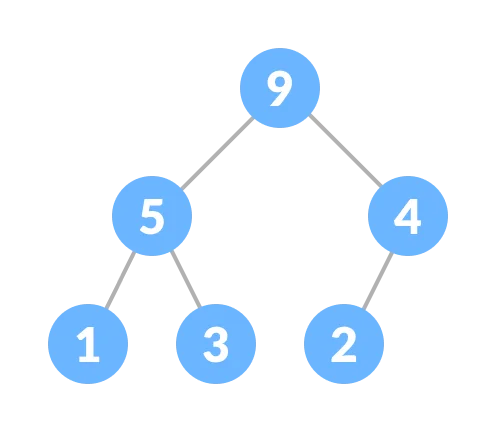
Max-Heap
3.2 Heap Operations
Heapify
Heapify is the process of creating a heap data structure from a binary tree. It is used to create a Min-Heap or a Max-Heap.
1. Let the input array be

Initial Array
2. Create a complete binary tree from the array
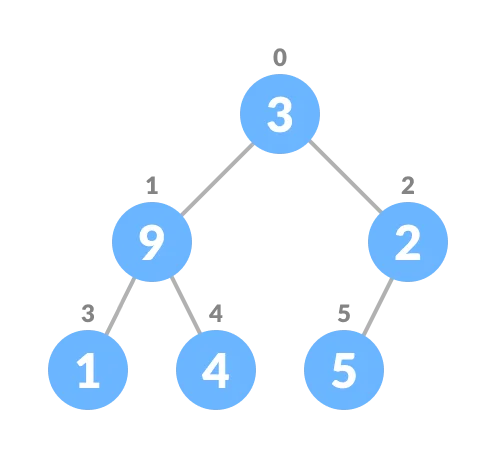
Complete binary tree
3. Start from the first index of non-leaf node whose index is given by n/2 - 1.
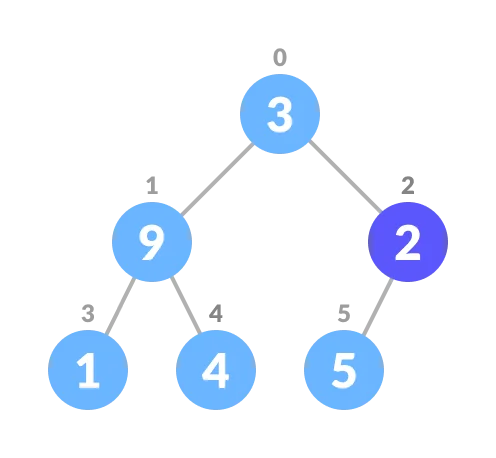
Start from the first on leaf node
4. Set current element i as largest.
5. The index of left child is given by 2i + 1 and the right child is given by 2i + 2.
If leftChild is greater than currentElement (i.e. element at ith index), set leftChildIndex as largest.
If rightChild is greater than element in largest, set rightChildIndex as largest.
6. Swap largest with currentElement.
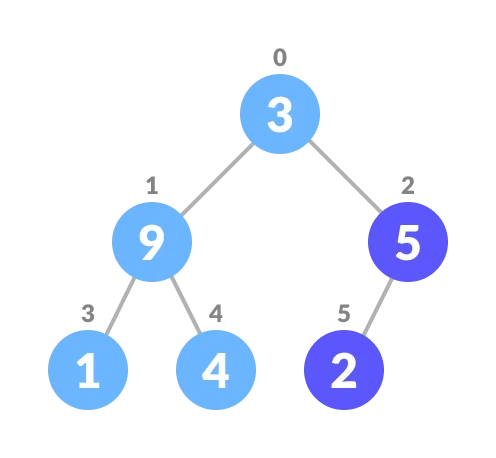
Swap if necessary
7. Repeat steps 3-7 until the subtrees are also heapified.
Algorithm
Heapify(array, size, i)
set i as largest
leftChild = 2i + 1
rightChild = 2i + 2
if leftChild > array[largest]
set leftChildIndex as largest
if rightChild > array[largest]
set rightChildIndex as largest
swap array[i] and array[largest]
To create a Max-Heap:
MaxHeap(array, size)
loop from the first index of non-leaf node down to zero
call heapify
For Min-Heap, both leftChild and rightChild must be larger than the parent for all nodes.
Insert
Algorithm for insertion in Max Heap
If there is no node,
create a newNode.
else (a node is already present)
insert the newNode at the end (last node from left to right.)
heapify the array
1. Insert the new element at the end of the tree.
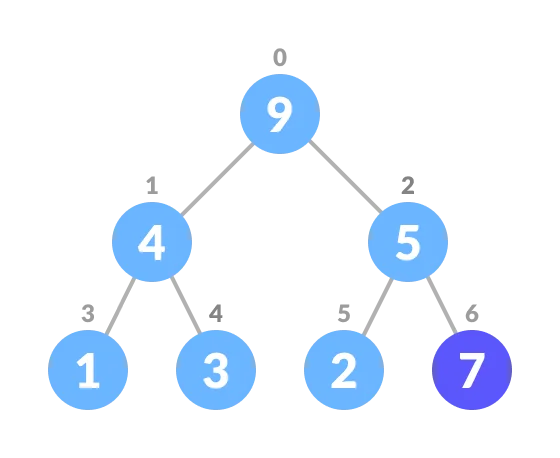
Insert at the end
2. Heapify the tree.
Heapify the array
For Min Heap, the above algorithm is modified so that parentNode is always smaller than newNode.
Delete
Algorithm for deletion in Max Heap
If nodeToBeDeleted is the leafNode
remove the node
Else swap nodeToBeDeleted with the lastLeafNode
remove noteToBeDeleted
heapify the array
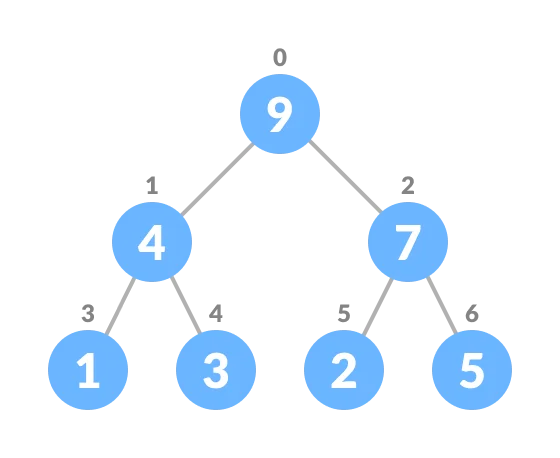
1.Select the element to be deleted.
Select the element to be deleted
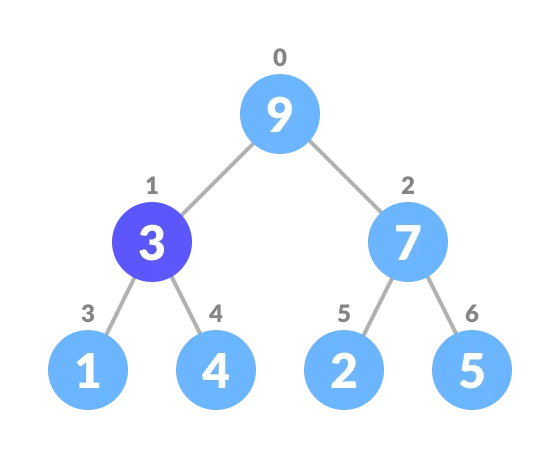
2.Swap it with the last element.
Swap with the last element
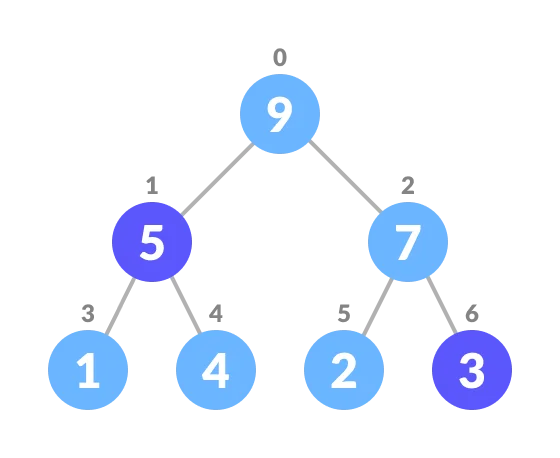
3.Remove the last element.
Remove the last element
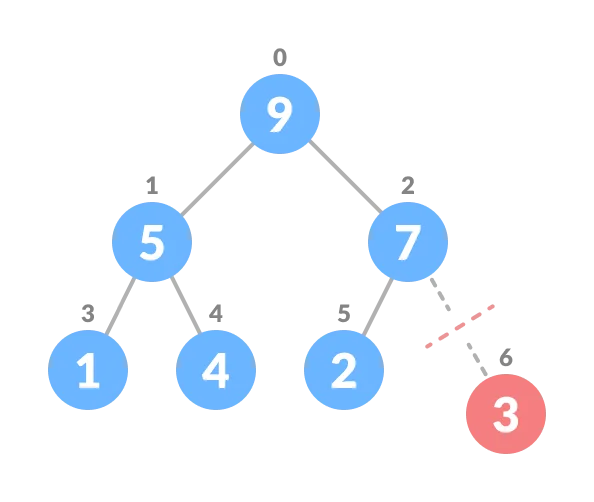
4.Heapify the tree.
Heapify the array
For Min Heap, above algorithm is modified so that both childNodes are greater smaller than currentNode.
Peek (Find max/min)
Peek operation returns the maximum element from Max Heap or minimum element from Min Heap without deleting the node.
For both Max heap and Min Heap
return rootNode
Extract Max/Min
Extract-Max returns the node with maximum value after removing it from a Max Heap whereas Extract-Min returns the node with minimum after removing it from Min Heap.
3.3 Heap Implementation
Min-Heap and Max-Heap data structure in Javascript
// title: 'MinHeap.js'
class MinHeap {
constructor () {
/* Initialing the array heap */
this.heap = []
}
getMin() {
/* Accessing the min element at index 1 in the heap array */
return this.heap[1]
}
getParentIdx(idx) {
return Math.floor((idx-1)/2)
}
insert(node) {
/* Inserting the new node at the end of the heap array */
this.heap.push(node)
/* Finding the correct position for the new node */
if (this.heap.length > 1) {
let idx = this.heap.length - 1
let parentIdx = this.getParentIdx(idx)
/* Traversing up the parent node until the current node (current) is greater than the parent */
while (parentIdx >= 0 && this.heap[idx] < this.heap[parentIdx]) {
/* Swapping the two nodes by using the ES6 destructuring syntax*/
[this.heap[parentIdx], this.heap[idx]] = [this.heap[idx], this.heap[parentIdx]]
idx = parentIdx
parentIdx = this.getParentIdx(idx);
}
}
return this.heap;
}
remove() {
[this.heap[0], this.heap[this.heap.length-1]] = [this.heap[this.heap.length-1], this.heap[0]]
this.heap.pop();
if (this.heap.length === 0) return [];
let idx;
let minIdx = 0;
while (idx !== minIdx) {
idx = minIdx;
let leftIdx = 2 * idx + 1;
let rightIdx = 2 * idx + 2;
if (leftIdx < this.heap.length && this.heap[leftIdx] < this.heap[minIdx]) {
minIdx = leftIdx;
}
if (rightIdx < this.heap.length && this.heap[rightIdx] < this.heap[minIdx]) {
minIdx = rightIdx;
}
[this.heap[idx], this.heap[minIdx]] = [this.heap[minIdx], this.heap[idx]]
}
return this.heap;
}
heapSort(arr) {
let minHeap = arr.reduce((heap, node) => {return this.insert(node)}, []);
let sorted = [];
while (minHeap.length>0) {
sorted.push(minHeap[0]);
minHeap = this.remove();
}
return sorted
};
};
let output = new MaxHeap()
console.log(output.heapSort([4, 10, 3, 5, 1])); // --> [1, 3, 4, 5, 10]
// title: 'MaxHeap.js'
class MaxHeap {
constructor () {
this.heap = []
}
getMax() {
return this.heap[1]
}
getParentIdx(idx) {
return Math.floor((idx-1)/2)
}
insert(node) {
this.heap.push(node)
if (this.heap.length > 1) {
let idx = this.heap.length - 1
let parentIdx = this.getParentIdx(idx)
while (parentIdx >= 0 && this.heap[parentIdx] < this.heap[idx]) {
[this.heap[parentIdx], this.heap[idx]] = [this.heap[idx], this.heap[parentIdx]]
idx = parentIdx
parentIdx = this.getParentIdx(idx);
}
}
return this.heap;
}
remove() {
[this.heap[0], this.heap[this.heap.length-1]] = [this.heap[this.heap.length-1], this.heap[0]]
this.heap.pop();
if (this.heap.length === 0) return [];
let idx;
let maxIdx = 0;
while (idx !== maxIdx) {
idx = maxIdx;
let leftIdx = 2 * idx + 1;
let rightIdx = 2 * idx + 2;
if (leftIdx < this.heap.length && this.heap[maxIdx] < this.heap[leftIdx]) {
maxIdx = leftIdx;
}
if (rightIdx < this.heap.length && this.heap[maxIdx] < this.heap[rightIdx]) {
maxIdx = rightIdx;
}
[this.heap[idx], this.heap[maxIdx]] = [this.heap[maxIdx], this.heap[idx]]
}
return this.heap;
}
heapSort(arr) {
let maxHeap = arr.reduce((heap, node) => {return this.insert(node)}, []);
let sorted = [];
while (maxHeap.length>0) {
sorted.push(maxHeap[0]);
maxHeap = this.remove();
}
return sorted
};
};
let output = new MaxHeap()
console.log(output.heapSort([4, 10, 3, 5, 1])); // --> [10, 5, 4, 3, 1]
Max-Heap data structure in Python
# title: 'MaxHeap.py'
def heapify(arr, n, i):
largest = i
l = 2 * i + 1
r = 2 * i + 2
if l < n and arr[i] < arr[l]:
largest = l
if r < n and arr[largest] < arr[r]:
largest = r
if largest != i:
arr[i],arr[largest] = arr[largest],arr[i]
heapify(arr, n, largest)
def insert(array, newNum):
size = len(array)
if size == 0:
array.append(newNum)
else:
array.append(newNum);
for i in range((size//2)-1, -1, -1):
heapify(array, size, i)
def deleteNode(array, num):
size = len(array)
i = 0
for i in range(0, size):
if num == array[i]:
break
array[i], array[size-1] = array[size-1], array[i]
array.remove(num)
for i in range((len(array)//2)-1, -1, -1):
heapify(array, len(array), i)
arr = []
insert(arr, 3)
insert(arr, 4)
insert(arr, 9)
insert(arr, 5)
insert(arr, 2)
print ("Max-Heap array: " + str(arr))
deleteNode(arr, 4)
print("After deleting an element: " + str(arr))
3.4 Heap Data Structure Applications
1. Implementing a priority queue.
2. Dijkstra’s Algorithm
3. Heap Sort
4. Trie
4.1 What is Trie?
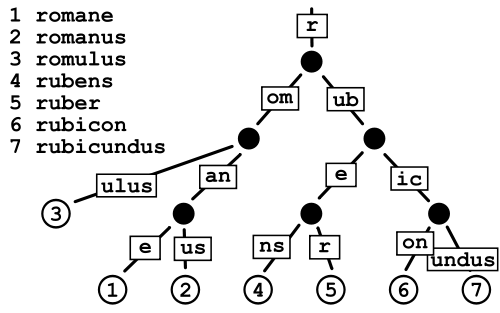
4.2 Trie Implementation
// title: 'Trie.js'
class Node {
constructor() {
this.keys = new Map();
this.end = false;
}
setEnd() {
this.end = true;
};
isEnd() {
return this.end;
};
}
class Trie {
constructor() {
this.root = new Node();
}
add(input, node = this.root) {
if (input.length == 0) {
node.setEnd();
return;
} else if (!node.keys.has(input[0])) {
node.keys.set(input[0], new Node());
return this.add(input.substr(1), node.keys.get(input[0]));
} else {
return this.add(input.substr(1), node.keys.get(input[0]));
};
};
isWord(word) {
let node = this.root;
while (word.length > 1) {
if (!node.keys.has(word[0])) {
return false;
} else {
node = node.keys.get(word[0]);
word = word.substr(1);
};
};
return (node.keys.has(word) && node.keys.get(word).isEnd()) ?
true : false;
};
print() {
let words = new Array();
let search = function(node, string) {
if (node.keys.size != 0) {
for (let letter of node.keys.keys()) {
search(node.keys.get(letter), string.concat(letter));
} if (node.isEnd()) {
words.push(string);
}
} else {
string.length > 0 ? words.push(string) : undefined;
return;
};
};
search(this.root, new String());
return words.length > 0 ? words : mo;
};
};
myTrie = new Trie()
myTrie.add('ball');
myTrie.add('bat');
myTrie.add('doll');
myTrie.add('dork');
myTrie.add('do');
myTrie.add('dorm')
myTrie.add('send')
myTrie.add('sense')
console.log(myTrie.isWord('doll')) // true
console.log(myTrie.isWord('dor')) // false
console.log(myTrie.isWord('dorf')) // false
console.log(myTrie.print()) // ['ball','bat','doll','dork','dorm','do','send','sense']
https://www.freecodecamp.org/
https://www.codesdope.com/
https://algorithmtutor.com/
https://blog.penjee.com/learnprogramming/programming-gifs/
https://dev.to/abdisalan_js/4-ways-to-traverse-binary-trees-with-animations-5bi5
https://www.programiz.com/